Monday, March 18, 2013
Review Section for Final.
TA TJ Torres will hold a special review section on Wednesday at 5 PM in ISB 231.
Sunday, March 17, 2013
Guide to the final.
Based on the feedback I have seen here, and my own ideas, I am thinking that things we could cover on the final include:
expectation values,
time dependence,
semiconductors,
pn junctions,
light emission (laser or led)
spin
re-organization of H-atom states due to fine-structure (s*L & p^4 terms).
Did I leave out anything? I'll be back later to post more about the final. In the mean time you could look at some of the final practice problems that seem to fit in well with these categories. (and practice doing them using just your equation sheet.) I would suggest maybe working backwards from 11 to 3. The last ones seem like the best place to start as they seem less difficult and more relevant.
The final exam schedule for winter quarter can be found here:
http://registrar.ucsc.edu/soc/final-examinations.html
My understanding is that for our class (TuTh, 2:00 PM) it is on Friday March 22 at 12:00 noon.
==========================
More notes on the final (March 20):
Most questions involve hydrogen atom states or 1DHO states. The others involve the nature of an LED (and Laser) and the origin of fine structure. A deep grasp of what states have time dependent expectation values will be of great value to you. The ability to calculate expectation values for both 1DHO and hydrogen atom states will also be emphasized. There are questions about fine-structure. There is one question from the midterm almost unchanged. I would suggest being prepared to do both 1D and 3D integrals. About 40 points involve integrals and expectation values. Reviewing the type of integrals you did to get the expectation value of x and y for hydrogen atom excited states will help with one problem.
If you can really understand problem 5, that will help you with one of the most difficult problems on the test.
Also, there is currently an extra-credit problem that is mostly about the 1DHO, but has a reference to gaussian wave-packet spreading (for $U(x) = 0$), which you covered last quarter. So you might want to recall that a bit, but the hard part of the problem is not that part, it is an extra-credit problem (and it is difficult) so I would not make that a main focus of your preparation, but just an extra thing after you have everything else down. Also, this problem might get bumped anyway if something better comes along. (Perhaps an extra credit problem on crystal states instead?)
Text above has been edited (March 20 10 PM). A few more thoughts:
Have an equation for fine structure energies ready...
expectation values,
time dependence,
semiconductors,
pn junctions,
light emission (laser or led)
spin
re-organization of H-atom states due to fine-structure (s*L & p^4 terms).
Did I leave out anything? I'll be back later to post more about the final. In the mean time you could look at some of the final practice problems that seem to fit in well with these categories. (and practice doing them using just your equation sheet.) I would suggest maybe working backwards from 11 to 3. The last ones seem like the best place to start as they seem less difficult and more relevant.
The final exam schedule for winter quarter can be found here:
http://registrar.ucsc.edu/soc/final-examinations.html
My understanding is that for our class (TuTh, 2:00 PM) it is on Friday March 22 at 12:00 noon.
==========================
More notes on the final (March 20):
Most questions involve hydrogen atom states or 1DHO states. The others involve the nature of an LED (and Laser) and the origin of fine structure. A deep grasp of what states have time dependent expectation values will be of great value to you. The ability to calculate expectation values for both 1DHO and hydrogen atom states will also be emphasized. There are questions about fine-structure. There is one question from the midterm almost unchanged. I would suggest being prepared to do both 1D and 3D integrals. About 40 points involve integrals and expectation values. Reviewing the type of integrals you did to get the expectation value of x and y for hydrogen atom excited states will help with one problem.
If you can really understand problem 5, that will help you with one of the most difficult problems on the test.
Also, there is currently an extra-credit problem that is mostly about the 1DHO, but has a reference to gaussian wave-packet spreading (for $U(x) = 0$), which you covered last quarter. So you might want to recall that a bit, but the hard part of the problem is not that part, it is an extra-credit problem (and it is difficult) so I would not make that a main focus of your preparation, but just an extra thing after you have everything else down. Also, this problem might get bumped anyway if something better comes along. (Perhaps an extra credit problem on crystal states instead?)
Text above has been edited (March 20 10 PM). A few more thoughts:
Have an equation for fine structure energies ready...
Wednesday, March 13, 2013
Tuesday, March 12, 2013
March 7 notes-part 2: Laser physics
I think in class on March 7, we discussed that, in the presence of the interaction term, $e E_x x cos (2 \pi f t)$ associated with a "photon", the coefficient for the excited state state is proportional to $\gamma t$, where
$\gamma = e E_x \int \psi_o (x) x \psi_1 (x) dx/\hbar$.
(Note that $e E_x x$ has units of energy (an interaction energy) and thus $e E_x x/\hbar$ has units of $sec^{-1}$.)
This indicates that the probability of an induced transition, which is proportional to $(\gamma t)^2$, is proportional to $(E_x)^2$, i.e, the energy in the electric field.
When considering an induced transition from the ground state to the first excited state, it makes intuitive sense that the probability of a transition is related to energy in the photon field (the number of photons). How could it be otherwise?
The key insight to understanding a laser is to realize that these equations are symmetric in the sense that they don't care whether the transition is up or down. The equations are unchanged if you interchange the initial and final states. Thus for an atom starting in the excited state, the probability of a downward transition to the ground state, in which a photon is emitted, is also proportional to $(E_x)^2$ (to the energy in the electric field). Thus, for a gas of atoms in an excited state, a passing resonant photon will tend to induce downward transitions, leading to photon emission, and then greater likelihood of emission from another atom. The strength of the electric field grows with each emission, that stimulates more emissions, etc. This leads to in-phase emissions of photons all traveling in the same direction. This is critical to how a laser works.
$\gamma = e E_x \int \psi_o (x) x \psi_1 (x) dx/\hbar$.
(Note that $e E_x x$ has units of energy (an interaction energy) and thus $e E_x x/\hbar$ has units of $sec^{-1}$.)
This indicates that the probability of an induced transition, which is proportional to $(\gamma t)^2$, is proportional to $(E_x)^2$, i.e, the energy in the electric field.
When considering an induced transition from the ground state to the first excited state, it makes intuitive sense that the probability of a transition is related to energy in the photon field (the number of photons). How could it be otherwise?
The key insight to understanding a laser is to realize that these equations are symmetric in the sense that they don't care whether the transition is up or down. The equations are unchanged if you interchange the initial and final states. Thus for an atom starting in the excited state, the probability of a downward transition to the ground state, in which a photon is emitted, is also proportional to $(E_x)^2$ (to the energy in the electric field). Thus, for a gas of atoms in an excited state, a passing resonant photon will tend to induce downward transitions, leading to photon emission, and then greater likelihood of emission from another atom. The strength of the electric field grows with each emission, that stimulates more emissions, etc. This leads to in-phase emissions of photons all traveling in the same direction. This is critical to how a laser works.
Monday, March 11, 2013
Final preparation problems.
Please keep posting more suggestions for problems. If you collaborate and participate then it is more likely that the final will not be incomprehensible and problems that are difficult to understand or pitched at the wrong level.
I'll post some easier problems later. I am still waiting for more feedback in the post "What would you like to see on the final."
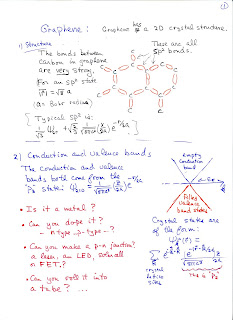
1) Consider a graphene sheet that is 2 mm long and 4 nm wide. Suppose that you dope the right half (Let's call that x>0) with donors to get a carrier density of 10^12 carriers/cm^2. Now suppose you role that into a 2mm long, narrow tube.
a) what is the radius of the tube?
b) what is the linear carrier density
c) If you apply an electric field that gives an (average) speed of 10^7 cm/sec to the carriers moving to the left, how many will arrive at the x=0 boundary per second?
2) With regard to the same half-doped graphene tube:
a) can the moving electron coming from the doped x>0 side cross the x=0 boundary? Why or why not? (the left half, x < 0, is undoped.)
b) will they fall into the valence band? why or why not?
c) If not, what do you need to do to enable them to drop into the valence band?
d) assuming you have solved part c) and that each one dropping into the valence band emits a photon,
how much radiated power would you get from one such "nanotube"... if the band gap were engineered to be 0.5 eV.
3. Previously we discussed that in the presence of an oscillating E-field of just the right frequency, the probability of a transition from one quantum state to another is proportional to the electric field squared times an integral of the wave-function of the initial state, the wave-function of the final state and x (where the x factor comes from the interaction potential $e E_x x$ (for an electric field polarized in the x direction). Starting from this, discuss how a laser works. Compare and contrast a laser and and LED made with the same semiconductor. What are the similarities and differences?
============
4. extra credit: a) Write the equation for a crystal state of wave-vector k (assuming you know the atom state that the crystal state evolves from). For a bandwidth of 4 eV, what is the velocity associated with theis crystal state? (Do you need to be given anything else to calculate that?)
c) Discuss what the animation below shows. [Hint: it is a Gaussian wave packet of crystal states center NOT at k=0. The packet is pretty narrow. This is for a 1D crystal with b=0.1 nm. Discuss: Around what k-value is this packet centered. How wide is it (in k and in x)? and other relevant things. Explain your reasoning. Please feel free and encouraged to discuss this here (in the comments).
.gif)
5. Consider an electron in a harmonic oscillator potential. Suppose that at t=0 it is in the state
$\Psi (x,0) = (c_o + c_1 x + c_2 x^2) e^{-x^2/2a^2}$.
a) Discuss the time dependence of this state? Is it time dependent?
b) How would you calculate $\bar{x}$? Would it depend on time?
6. Referring to hydrogen atom states,
a) write the state $\psi_{2,1,3/2,1/2}$ in terms of $\psi_{n.l.m}$ states (with spin).
b) extra credit: write the state $\psi_{2,1,3/2,1/2}$ in terms of $\psi_{2x}$ type states (with spin).
7. Suppose an electron in a hydrogen atom is in a state that is an equal mix of the ground state and 1st excited state. Pick a particular 1st excited state and for your choice:
a) Describe/discuss what you would expect to get if you calculated $\bar{x}$, $\bar{y}$ and $\bar{z}$ (include a graph or graphs) in your description.
b) Calculate $\bar{x}$, $\bar{y}$ and $\bar{z}$ (include a graph or graphs).
8. Describe a p-n junction and how it can be used to create an LED or laser. Which way do the electrons flow? what happens? etc extra credit for elucidating the difference between an LED and a Laser.
9. For an electron in a harmonic oscillator potential that is in a state that is an equal mix of the ground state and 1st excited state,
a) calculate and graph $\bar{x}$? Would it depend on time?
10. Same as 9, but instead of an equal mix suppose that the coefficient of the g.s. term is 0.9.
a) calculate and graph $\bar{x}$? Compare your results from 9 and 10.
10.1 Same as 9, but instead of an equal mix suppose that the coefficient of the g.s. term is 0.99.
a) What is the coefficient of the 1st-excited state?
b) calculate and graph $\bar{x}$? Compare your results from 9 and 10.
11. Suppose you have a biased (forward) p-n junction with a junction area of 0.1 cm^2. If the average electron speed is 5 x 10^6 cm/sec and the electron density is 10^17/cm^3, how much power would be radiated in either an LED or Laser (assume 100% efficiency). You can assume an equal and opposite flow of holes from the p side to the n side.
12. For an electron in the ground state of an infinite square well of width 0.5 nm, what is the expectation value in eV of:
a) the kinetic energy,
b) the potential energy.
c) why does an electron in a well have kinetic energy?
13. Consider a finite square well of depth 20 eV that has exactly (only) 3 bound states. One is 2.5 eV above the energy of the bottom of the well, the next 9 eV (same reference) and the 3rd at 17 eV.
a) sketch the states.
b) Describe and sketch the optical absorption spectrum that you would predict for this system. Label all sharp lines corresponding to transitions with their initial and final states and indicate their energy.
c) Assuming the strength of any transition is related to x integrated with the initial and final states, which transitions would be unobservable?
.gif)
I'll post some easier problems later. I am still waiting for more feedback in the post "What would you like to see on the final."
1) Consider a graphene sheet that is 2 mm long and 4 nm wide. Suppose that you dope the right half (Let's call that x>0) with donors to get a carrier density of 10^12 carriers/cm^2. Now suppose you role that into a 2mm long, narrow tube.
a) what is the radius of the tube?
b) what is the linear carrier density
c) If you apply an electric field that gives an (average) speed of 10^7 cm/sec to the carriers moving to the left, how many will arrive at the x=0 boundary per second?
2) With regard to the same half-doped graphene tube:
a) can the moving electron coming from the doped x>0 side cross the x=0 boundary? Why or why not? (the left half, x < 0, is undoped.)
b) will they fall into the valence band? why or why not?
c) If not, what do you need to do to enable them to drop into the valence band?
d) assuming you have solved part c) and that each one dropping into the valence band emits a photon,
how much radiated power would you get from one such "nanotube"... if the band gap were engineered to be 0.5 eV.
3. Previously we discussed that in the presence of an oscillating E-field of just the right frequency, the probability of a transition from one quantum state to another is proportional to the electric field squared times an integral of the wave-function of the initial state, the wave-function of the final state and x (where the x factor comes from the interaction potential $e E_x x$ (for an electric field polarized in the x direction). Starting from this, discuss how a laser works. Compare and contrast a laser and and LED made with the same semiconductor. What are the similarities and differences?
============
4. extra credit: a) Write the equation for a crystal state of wave-vector k (assuming you know the atom state that the crystal state evolves from). For a bandwidth of 4 eV, what is the velocity associated with theis crystal state? (Do you need to be given anything else to calculate that?)
c) Discuss what the animation below shows. [Hint: it is a Gaussian wave packet of crystal states center NOT at k=0. The packet is pretty narrow. This is for a 1D crystal with b=0.1 nm. Discuss: Around what k-value is this packet centered. How wide is it (in k and in x)? and other relevant things. Explain your reasoning. Please feel free and encouraged to discuss this here (in the comments).
.gif)
5. Consider an electron in a harmonic oscillator potential. Suppose that at t=0 it is in the state
$\Psi (x,0) = (c_o + c_1 x + c_2 x^2) e^{-x^2/2a^2}$.
a) Discuss the time dependence of this state? Is it time dependent?
b) How would you calculate $\bar{x}$? Would it depend on time?
6. Referring to hydrogen atom states,
a) write the state $\psi_{2,1,3/2,1/2}$ in terms of $\psi_{n.l.m}$ states (with spin).
b) extra credit: write the state $\psi_{2,1,3/2,1/2}$ in terms of $\psi_{2x}$ type states (with spin).
7. Suppose an electron in a hydrogen atom is in a state that is an equal mix of the ground state and 1st excited state. Pick a particular 1st excited state and for your choice:
a) Describe/discuss what you would expect to get if you calculated $\bar{x}$, $\bar{y}$ and $\bar{z}$ (include a graph or graphs) in your description.
b) Calculate $\bar{x}$, $\bar{y}$ and $\bar{z}$ (include a graph or graphs).
8. Describe a p-n junction and how it can be used to create an LED or laser. Which way do the electrons flow? what happens? etc extra credit for elucidating the difference between an LED and a Laser.
9. For an electron in a harmonic oscillator potential that is in a state that is an equal mix of the ground state and 1st excited state,
a) calculate and graph $\bar{x}$? Would it depend on time?
10. Same as 9, but instead of an equal mix suppose that the coefficient of the g.s. term is 0.9.
a) calculate and graph $\bar{x}$? Compare your results from 9 and 10.
10.1 Same as 9, but instead of an equal mix suppose that the coefficient of the g.s. term is 0.99.
a) What is the coefficient of the 1st-excited state?
b) calculate and graph $\bar{x}$? Compare your results from 9 and 10.
11. Suppose you have a biased (forward) p-n junction with a junction area of 0.1 cm^2. If the average electron speed is 5 x 10^6 cm/sec and the electron density is 10^17/cm^3, how much power would be radiated in either an LED or Laser (assume 100% efficiency). You can assume an equal and opposite flow of holes from the p side to the n side.
12. For an electron in the ground state of an infinite square well of width 0.5 nm, what is the expectation value in eV of:
a) the kinetic energy,
b) the potential energy.
c) why does an electron in a well have kinetic energy?
13. Consider a finite square well of depth 20 eV that has exactly (only) 3 bound states. One is 2.5 eV above the energy of the bottom of the well, the next 9 eV (same reference) and the 3rd at 17 eV.
a) sketch the states.
b) Describe and sketch the optical absorption spectrum that you would predict for this system. Label all sharp lines corresponding to transitions with their initial and final states and indicate their energy.
c) Assuming the strength of any transition is related to x integrated with the initial and final states, which transitions would be unobservable?
.gif)
Friday, March 8, 2013
What would you like to see on the final?
The goal of this post is to get a sense of what you would like to see on the final, as well as what you might not like to see. Your comments do not have to be in the form of full detailed questions. They can just be brief mention of what sort of problems, what areas, you think should be covered on the final (and what should not be). Feel free to share your reasoning or not. Either way I would be very interested in your thoughts on this important question.
Saturday, March 2, 2013
Thursday March 7 notes. Quantum transitions and mixed states.
The theoretical result that the probability of emitting a photon is proportional to the oscillating electric field (squared) at the "resonant" frequency, means that (slipping into photon language) a photon going by an excited atom makes it more likely for that atom to emit another identical photon. Laser physics is a confirmation of this theoretical concept and prediction.
In absorption spectroscopy, if an incoming photon has an energy that coincides pretty exactly with the difference in energy between two quantum states, then it can stimulate a transition between those states. Actually one does not represent the photon in a quantum manner, but rather as a (classical) electric field oscillating at a frequency f. When the oscillation frequency is "tuned" so that $\hbar 2 \pi f = E_1 - E_o$, the oscillating electric field can stimulate a transition between a state of energy $E_o$ and a state of energy $E_1$. In that case the state may be of the unusual time dependent form
$\Psi(x,t) = (1-\gamma^2 t^2)^{1/2} \Psi_o(x,t) + \gamma t \Psi_1(x,t)$, where, because of the time dependence of the interaction potential one gets time dependent coefficients in front of the "before"state and "after" state.
Perhaps one can think of it this way. At t=0, the electron is purely in the ground state. And I should have mentioned before, let's also suppose that before t=0 the electron is just in the ground state, and then at t=0 the time dependent interaction term appears. Then the state will begin to evolve from a pure state into mixed state with an increasing amount of 1st excited state mixed in. Really this approach is only good for a fairly short range of time, from t=0 to about $\gamma t = 0.2$.
Let's see, what can we say about this and what does it seem to show us?
1) Well first maybe we should mention again that the first excited state was selected to be the 2nd energy eigenstate in the mixed state by the "tuning" of the frequency of the oscillating electric field to just the right frequency $2 \pi f = (E_1 - E_o)/\hbar = \omega_1 - \omega_o$.
2) Second, what one calls a quantum jump (from the $E_o$ to $E_1$ state) is not really sudden at all, in our formulation, but rather a continuous evolution of the state due to the influence of the E field.
3) Third, there presumably is a jump at some point. How does that happen? How should we think about that?... Let's take the example of an Mg atom in a photosynthetic molecule. Suppose it starts out in its ground state and an oscillating electric field puts the Mg+ valence electron into a mixed state, as outlined above. The resolution of the energy of the mixed state, in this case and in all cases, is associated with some interaction with the environment outside the atom. In the case of a photosynthetic molecule, the Mg atom is connected to a pretty complex molecular environment via two nitrogen atoms. Once its excited valence electron travels across one of those nitrogen bridges, to begin its photosynthesis journey, the mixed state is over. The probability for the electron to start that journey is related to the coefficient of the 1st excited state in the above mixed state. In that sense one can say that the electron was induced to jump to the excited state and that that was essential to its beginning its travels. Also, the energy lost by the electromagetic field, hf, is equal to the energy gained by the electron.
The resolution of a mixed state, into one energy or the other, tends to involve an interaction between our simple quantum system, which we can model and describe pretty well, and a quite complex environment, which is difficult (or impossible) to model with any precision.
Ideas like wave-function collapse do not have any actual theory behind them. Most physicists in the current era do not believe in anything like that in my experience.
Subscribe to:
Posts (Atom)