Monday, March 18, 2013
Review Section for Final.
TA TJ Torres will hold a special review section on Wednesday at 5 PM in ISB 231.
Sunday, March 17, 2013
Guide to the final.
Based on the feedback I have seen here, and my own ideas, I am thinking that things we could cover on the final include:
expectation values,
time dependence,
semiconductors,
pn junctions,
light emission (laser or led)
spin
re-organization of H-atom states due to fine-structure (s*L & p^4 terms).
Did I leave out anything? I'll be back later to post more about the final. In the mean time you could look at some of the final practice problems that seem to fit in well with these categories. (and practice doing them using just your equation sheet.) I would suggest maybe working backwards from 11 to 3. The last ones seem like the best place to start as they seem less difficult and more relevant.
The final exam schedule for winter quarter can be found here:
http://registrar.ucsc.edu/soc/final-examinations.html
My understanding is that for our class (TuTh, 2:00 PM) it is on Friday March 22 at 12:00 noon.
==========================
More notes on the final (March 20):
Most questions involve hydrogen atom states or 1DHO states. The others involve the nature of an LED (and Laser) and the origin of fine structure. A deep grasp of what states have time dependent expectation values will be of great value to you. The ability to calculate expectation values for both 1DHO and hydrogen atom states will also be emphasized. There are questions about fine-structure. There is one question from the midterm almost unchanged. I would suggest being prepared to do both 1D and 3D integrals. About 40 points involve integrals and expectation values. Reviewing the type of integrals you did to get the expectation value of x and y for hydrogen atom excited states will help with one problem.
If you can really understand problem 5, that will help you with one of the most difficult problems on the test.
Also, there is currently an extra-credit problem that is mostly about the 1DHO, but has a reference to gaussian wave-packet spreading (for $U(x) = 0$), which you covered last quarter. So you might want to recall that a bit, but the hard part of the problem is not that part, it is an extra-credit problem (and it is difficult) so I would not make that a main focus of your preparation, but just an extra thing after you have everything else down. Also, this problem might get bumped anyway if something better comes along. (Perhaps an extra credit problem on crystal states instead?)
Text above has been edited (March 20 10 PM). A few more thoughts:
Have an equation for fine structure energies ready...
expectation values,
time dependence,
semiconductors,
pn junctions,
light emission (laser or led)
spin
re-organization of H-atom states due to fine-structure (s*L & p^4 terms).
Did I leave out anything? I'll be back later to post more about the final. In the mean time you could look at some of the final practice problems that seem to fit in well with these categories. (and practice doing them using just your equation sheet.) I would suggest maybe working backwards from 11 to 3. The last ones seem like the best place to start as they seem less difficult and more relevant.
The final exam schedule for winter quarter can be found here:
http://registrar.ucsc.edu/soc/final-examinations.html
My understanding is that for our class (TuTh, 2:00 PM) it is on Friday March 22 at 12:00 noon.
==========================
More notes on the final (March 20):
Most questions involve hydrogen atom states or 1DHO states. The others involve the nature of an LED (and Laser) and the origin of fine structure. A deep grasp of what states have time dependent expectation values will be of great value to you. The ability to calculate expectation values for both 1DHO and hydrogen atom states will also be emphasized. There are questions about fine-structure. There is one question from the midterm almost unchanged. I would suggest being prepared to do both 1D and 3D integrals. About 40 points involve integrals and expectation values. Reviewing the type of integrals you did to get the expectation value of x and y for hydrogen atom excited states will help with one problem.
If you can really understand problem 5, that will help you with one of the most difficult problems on the test.
Also, there is currently an extra-credit problem that is mostly about the 1DHO, but has a reference to gaussian wave-packet spreading (for $U(x) = 0$), which you covered last quarter. So you might want to recall that a bit, but the hard part of the problem is not that part, it is an extra-credit problem (and it is difficult) so I would not make that a main focus of your preparation, but just an extra thing after you have everything else down. Also, this problem might get bumped anyway if something better comes along. (Perhaps an extra credit problem on crystal states instead?)
Text above has been edited (March 20 10 PM). A few more thoughts:
Have an equation for fine structure energies ready...
Wednesday, March 13, 2013
Tuesday, March 12, 2013
March 7 notes-part 2: Laser physics
I think in class on March 7, we discussed that, in the presence of the interaction term, $e E_x x cos (2 \pi f t)$ associated with a "photon", the coefficient for the excited state state is proportional to $\gamma t$, where
$\gamma = e E_x \int \psi_o (x) x \psi_1 (x) dx/\hbar$.
(Note that $e E_x x$ has units of energy (an interaction energy) and thus $e E_x x/\hbar$ has units of $sec^{-1}$.)
This indicates that the probability of an induced transition, which is proportional to $(\gamma t)^2$, is proportional to $(E_x)^2$, i.e, the energy in the electric field.
When considering an induced transition from the ground state to the first excited state, it makes intuitive sense that the probability of a transition is related to energy in the photon field (the number of photons). How could it be otherwise?
The key insight to understanding a laser is to realize that these equations are symmetric in the sense that they don't care whether the transition is up or down. The equations are unchanged if you interchange the initial and final states. Thus for an atom starting in the excited state, the probability of a downward transition to the ground state, in which a photon is emitted, is also proportional to $(E_x)^2$ (to the energy in the electric field). Thus, for a gas of atoms in an excited state, a passing resonant photon will tend to induce downward transitions, leading to photon emission, and then greater likelihood of emission from another atom. The strength of the electric field grows with each emission, that stimulates more emissions, etc. This leads to in-phase emissions of photons all traveling in the same direction. This is critical to how a laser works.
$\gamma = e E_x \int \psi_o (x) x \psi_1 (x) dx/\hbar$.
(Note that $e E_x x$ has units of energy (an interaction energy) and thus $e E_x x/\hbar$ has units of $sec^{-1}$.)
This indicates that the probability of an induced transition, which is proportional to $(\gamma t)^2$, is proportional to $(E_x)^2$, i.e, the energy in the electric field.
When considering an induced transition from the ground state to the first excited state, it makes intuitive sense that the probability of a transition is related to energy in the photon field (the number of photons). How could it be otherwise?
The key insight to understanding a laser is to realize that these equations are symmetric in the sense that they don't care whether the transition is up or down. The equations are unchanged if you interchange the initial and final states. Thus for an atom starting in the excited state, the probability of a downward transition to the ground state, in which a photon is emitted, is also proportional to $(E_x)^2$ (to the energy in the electric field). Thus, for a gas of atoms in an excited state, a passing resonant photon will tend to induce downward transitions, leading to photon emission, and then greater likelihood of emission from another atom. The strength of the electric field grows with each emission, that stimulates more emissions, etc. This leads to in-phase emissions of photons all traveling in the same direction. This is critical to how a laser works.
Monday, March 11, 2013
Final preparation problems.
Please keep posting more suggestions for problems. If you collaborate and participate then it is more likely that the final will not be incomprehensible and problems that are difficult to understand or pitched at the wrong level.
I'll post some easier problems later. I am still waiting for more feedback in the post "What would you like to see on the final."
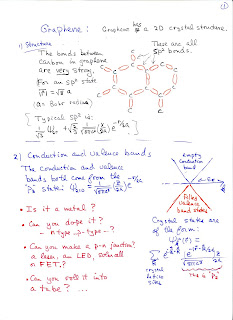
1) Consider a graphene sheet that is 2 mm long and 4 nm wide. Suppose that you dope the right half (Let's call that x>0) with donors to get a carrier density of 10^12 carriers/cm^2. Now suppose you role that into a 2mm long, narrow tube.
a) what is the radius of the tube?
b) what is the linear carrier density
c) If you apply an electric field that gives an (average) speed of 10^7 cm/sec to the carriers moving to the left, how many will arrive at the x=0 boundary per second?
2) With regard to the same half-doped graphene tube:
a) can the moving electron coming from the doped x>0 side cross the x=0 boundary? Why or why not? (the left half, x < 0, is undoped.)
b) will they fall into the valence band? why or why not?
c) If not, what do you need to do to enable them to drop into the valence band?
d) assuming you have solved part c) and that each one dropping into the valence band emits a photon,
how much radiated power would you get from one such "nanotube"... if the band gap were engineered to be 0.5 eV.
3. Previously we discussed that in the presence of an oscillating E-field of just the right frequency, the probability of a transition from one quantum state to another is proportional to the electric field squared times an integral of the wave-function of the initial state, the wave-function of the final state and x (where the x factor comes from the interaction potential $e E_x x$ (for an electric field polarized in the x direction). Starting from this, discuss how a laser works. Compare and contrast a laser and and LED made with the same semiconductor. What are the similarities and differences?
============
4. extra credit: a) Write the equation for a crystal state of wave-vector k (assuming you know the atom state that the crystal state evolves from). For a bandwidth of 4 eV, what is the velocity associated with theis crystal state? (Do you need to be given anything else to calculate that?)
c) Discuss what the animation below shows. [Hint: it is a Gaussian wave packet of crystal states center NOT at k=0. The packet is pretty narrow. This is for a 1D crystal with b=0.1 nm. Discuss: Around what k-value is this packet centered. How wide is it (in k and in x)? and other relevant things. Explain your reasoning. Please feel free and encouraged to discuss this here (in the comments).
.gif)
5. Consider an electron in a harmonic oscillator potential. Suppose that at t=0 it is in the state
$\Psi (x,0) = (c_o + c_1 x + c_2 x^2) e^{-x^2/2a^2}$.
a) Discuss the time dependence of this state? Is it time dependent?
b) How would you calculate $\bar{x}$? Would it depend on time?
6. Referring to hydrogen atom states,
a) write the state $\psi_{2,1,3/2,1/2}$ in terms of $\psi_{n.l.m}$ states (with spin).
b) extra credit: write the state $\psi_{2,1,3/2,1/2}$ in terms of $\psi_{2x}$ type states (with spin).
7. Suppose an electron in a hydrogen atom is in a state that is an equal mix of the ground state and 1st excited state. Pick a particular 1st excited state and for your choice:
a) Describe/discuss what you would expect to get if you calculated $\bar{x}$, $\bar{y}$ and $\bar{z}$ (include a graph or graphs) in your description.
b) Calculate $\bar{x}$, $\bar{y}$ and $\bar{z}$ (include a graph or graphs).
8. Describe a p-n junction and how it can be used to create an LED or laser. Which way do the electrons flow? what happens? etc extra credit for elucidating the difference between an LED and a Laser.
9. For an electron in a harmonic oscillator potential that is in a state that is an equal mix of the ground state and 1st excited state,
a) calculate and graph $\bar{x}$? Would it depend on time?
10. Same as 9, but instead of an equal mix suppose that the coefficient of the g.s. term is 0.9.
a) calculate and graph $\bar{x}$? Compare your results from 9 and 10.
10.1 Same as 9, but instead of an equal mix suppose that the coefficient of the g.s. term is 0.99.
a) What is the coefficient of the 1st-excited state?
b) calculate and graph $\bar{x}$? Compare your results from 9 and 10.
11. Suppose you have a biased (forward) p-n junction with a junction area of 0.1 cm^2. If the average electron speed is 5 x 10^6 cm/sec and the electron density is 10^17/cm^3, how much power would be radiated in either an LED or Laser (assume 100% efficiency). You can assume an equal and opposite flow of holes from the p side to the n side.
12. For an electron in the ground state of an infinite square well of width 0.5 nm, what is the expectation value in eV of:
a) the kinetic energy,
b) the potential energy.
c) why does an electron in a well have kinetic energy?
13. Consider a finite square well of depth 20 eV that has exactly (only) 3 bound states. One is 2.5 eV above the energy of the bottom of the well, the next 9 eV (same reference) and the 3rd at 17 eV.
a) sketch the states.
b) Describe and sketch the optical absorption spectrum that you would predict for this system. Label all sharp lines corresponding to transitions with their initial and final states and indicate their energy.
c) Assuming the strength of any transition is related to x integrated with the initial and final states, which transitions would be unobservable?
.gif)
I'll post some easier problems later. I am still waiting for more feedback in the post "What would you like to see on the final."
1) Consider a graphene sheet that is 2 mm long and 4 nm wide. Suppose that you dope the right half (Let's call that x>0) with donors to get a carrier density of 10^12 carriers/cm^2. Now suppose you role that into a 2mm long, narrow tube.
a) what is the radius of the tube?
b) what is the linear carrier density
c) If you apply an electric field that gives an (average) speed of 10^7 cm/sec to the carriers moving to the left, how many will arrive at the x=0 boundary per second?
2) With regard to the same half-doped graphene tube:
a) can the moving electron coming from the doped x>0 side cross the x=0 boundary? Why or why not? (the left half, x < 0, is undoped.)
b) will they fall into the valence band? why or why not?
c) If not, what do you need to do to enable them to drop into the valence band?
d) assuming you have solved part c) and that each one dropping into the valence band emits a photon,
how much radiated power would you get from one such "nanotube"... if the band gap were engineered to be 0.5 eV.
3. Previously we discussed that in the presence of an oscillating E-field of just the right frequency, the probability of a transition from one quantum state to another is proportional to the electric field squared times an integral of the wave-function of the initial state, the wave-function of the final state and x (where the x factor comes from the interaction potential $e E_x x$ (for an electric field polarized in the x direction). Starting from this, discuss how a laser works. Compare and contrast a laser and and LED made with the same semiconductor. What are the similarities and differences?
============
4. extra credit: a) Write the equation for a crystal state of wave-vector k (assuming you know the atom state that the crystal state evolves from). For a bandwidth of 4 eV, what is the velocity associated with theis crystal state? (Do you need to be given anything else to calculate that?)
c) Discuss what the animation below shows. [Hint: it is a Gaussian wave packet of crystal states center NOT at k=0. The packet is pretty narrow. This is for a 1D crystal with b=0.1 nm. Discuss: Around what k-value is this packet centered. How wide is it (in k and in x)? and other relevant things. Explain your reasoning. Please feel free and encouraged to discuss this here (in the comments).
.gif)
5. Consider an electron in a harmonic oscillator potential. Suppose that at t=0 it is in the state
$\Psi (x,0) = (c_o + c_1 x + c_2 x^2) e^{-x^2/2a^2}$.
a) Discuss the time dependence of this state? Is it time dependent?
b) How would you calculate $\bar{x}$? Would it depend on time?
6. Referring to hydrogen atom states,
a) write the state $\psi_{2,1,3/2,1/2}$ in terms of $\psi_{n.l.m}$ states (with spin).
b) extra credit: write the state $\psi_{2,1,3/2,1/2}$ in terms of $\psi_{2x}$ type states (with spin).
7. Suppose an electron in a hydrogen atom is in a state that is an equal mix of the ground state and 1st excited state. Pick a particular 1st excited state and for your choice:
a) Describe/discuss what you would expect to get if you calculated $\bar{x}$, $\bar{y}$ and $\bar{z}$ (include a graph or graphs) in your description.
b) Calculate $\bar{x}$, $\bar{y}$ and $\bar{z}$ (include a graph or graphs).
8. Describe a p-n junction and how it can be used to create an LED or laser. Which way do the electrons flow? what happens? etc extra credit for elucidating the difference between an LED and a Laser.
9. For an electron in a harmonic oscillator potential that is in a state that is an equal mix of the ground state and 1st excited state,
a) calculate and graph $\bar{x}$? Would it depend on time?
10. Same as 9, but instead of an equal mix suppose that the coefficient of the g.s. term is 0.9.
a) calculate and graph $\bar{x}$? Compare your results from 9 and 10.
10.1 Same as 9, but instead of an equal mix suppose that the coefficient of the g.s. term is 0.99.
a) What is the coefficient of the 1st-excited state?
b) calculate and graph $\bar{x}$? Compare your results from 9 and 10.
11. Suppose you have a biased (forward) p-n junction with a junction area of 0.1 cm^2. If the average electron speed is 5 x 10^6 cm/sec and the electron density is 10^17/cm^3, how much power would be radiated in either an LED or Laser (assume 100% efficiency). You can assume an equal and opposite flow of holes from the p side to the n side.
12. For an electron in the ground state of an infinite square well of width 0.5 nm, what is the expectation value in eV of:
a) the kinetic energy,
b) the potential energy.
c) why does an electron in a well have kinetic energy?
13. Consider a finite square well of depth 20 eV that has exactly (only) 3 bound states. One is 2.5 eV above the energy of the bottom of the well, the next 9 eV (same reference) and the 3rd at 17 eV.
a) sketch the states.
b) Describe and sketch the optical absorption spectrum that you would predict for this system. Label all sharp lines corresponding to transitions with their initial and final states and indicate their energy.
c) Assuming the strength of any transition is related to x integrated with the initial and final states, which transitions would be unobservable?
.gif)
Friday, March 8, 2013
What would you like to see on the final?
The goal of this post is to get a sense of what you would like to see on the final, as well as what you might not like to see. Your comments do not have to be in the form of full detailed questions. They can just be brief mention of what sort of problems, what areas, you think should be covered on the final (and what should not be). Feel free to share your reasoning or not. Either way I would be very interested in your thoughts on this important question.
Saturday, March 2, 2013
Thursday March 7 notes. Quantum transitions and mixed states.
Here is something new. This may help us understand spectroscopy. It also lays the foundation for understanding lasers. In particular, the concept of stimulated emission, which is critical to a laser, comes from the result, embedded in this calculation, that the probability of an induced transition is proportional to the square of the electric field amplitude at the frequency of the photon that would be emitted or absorbed in the transition. The direction of the transition, up or down, makes no difference. All transitions are stimulated. There is no such thing as a spontaneous transition.
The theoretical result that the probability of emitting a photon is proportional to the oscillating electric field (squared) at the "resonant" frequency, means that (slipping into photon language) a photon going by an excited atom makes it more likely for that atom to emit another identical photon. Laser physics is a confirmation of this theoretical concept and prediction.
In absorption spectroscopy, if an incoming photon has an energy that coincides pretty exactly with the difference in energy between two quantum states, then it can stimulate a transition between those states. Actually one does not represent the photon in a quantum manner, but rather as a (classical) electric field oscillating at a frequency f. When the oscillation frequency is "tuned" so that $\hbar 2 \pi f = E_1 - E_o$, the oscillating electric field can stimulate a transition between a state of energy $E_o$ and a state of energy $E_1$. In that case the state may be of the unusual time dependent form
$\Psi(x,t) = (1-\gamma^2 t^2)^{1/2} \Psi_o(x,t) + \gamma t \Psi_1(x,t)$, where, because of the time dependence of the interaction potential one gets time dependent coefficients in front of the "before"state and "after" state.
Perhaps one can think of it this way. At t=0, the electron is purely in the ground state. And I should have mentioned before, let's also suppose that before t=0 the electron is just in the ground state, and then at t=0 the time dependent interaction term appears. Then the state will begin to evolve from a pure state into mixed state with an increasing amount of 1st excited state mixed in. Really this approach is only good for a fairly short range of time, from t=0 to about $\gamma t = 0.2$.
Let's see, what can we say about this and what does it seem to show us?
1) Well first maybe we should mention again that the first excited state was selected to be the 2nd energy eigenstate in the mixed state by the "tuning" of the frequency of the oscillating electric field to just the right frequency $2 \pi f = (E_1 - E_o)/\hbar = \omega_1 - \omega_o$.
2) Second, what one calls a quantum jump (from the $E_o$ to $E_1$ state) is not really sudden at all, in our formulation, but rather a continuous evolution of the state due to the influence of the E field.
3) Third, there presumably is a jump at some point. How does that happen? How should we think about that?... Let's take the example of an Mg atom in a photosynthetic molecule. Suppose it starts out in its ground state and an oscillating electric field puts the Mg+ valence electron into a mixed state, as outlined above. The resolution of the energy of the mixed state, in this case and in all cases, is associated with some interaction with the environment outside the atom. In the case of a photosynthetic molecule, the Mg atom is connected to a pretty complex molecular environment via two nitrogen atoms. Once its excited valence electron travels across one of those nitrogen bridges, to begin its photosynthesis journey, the mixed state is over. The probability for the electron to start that journey is related to the coefficient of the 1st excited state in the above mixed state. In that sense one can say that the electron was induced to jump to the excited state and that that was essential to its beginning its travels. Also, the energy lost by the electromagetic field, hf, is equal to the energy gained by the electron.
The resolution of a mixed state, into one energy or the other, tends to involve an interaction between our simple quantum system, which we can model and describe pretty well, and a quite complex environment, which is difficult (or impossible) to model with any precision.
Ideas like wave-function collapse do not have any actual theory behind them. Most physicists in the current era do not believe in anything like that in my experience.
The theoretical result that the probability of emitting a photon is proportional to the oscillating electric field (squared) at the "resonant" frequency, means that (slipping into photon language) a photon going by an excited atom makes it more likely for that atom to emit another identical photon. Laser physics is a confirmation of this theoretical concept and prediction.
In absorption spectroscopy, if an incoming photon has an energy that coincides pretty exactly with the difference in energy between two quantum states, then it can stimulate a transition between those states. Actually one does not represent the photon in a quantum manner, but rather as a (classical) electric field oscillating at a frequency f. When the oscillation frequency is "tuned" so that $\hbar 2 \pi f = E_1 - E_o$, the oscillating electric field can stimulate a transition between a state of energy $E_o$ and a state of energy $E_1$. In that case the state may be of the unusual time dependent form
$\Psi(x,t) = (1-\gamma^2 t^2)^{1/2} \Psi_o(x,t) + \gamma t \Psi_1(x,t)$, where, because of the time dependence of the interaction potential one gets time dependent coefficients in front of the "before"state and "after" state.
Perhaps one can think of it this way. At t=0, the electron is purely in the ground state. And I should have mentioned before, let's also suppose that before t=0 the electron is just in the ground state, and then at t=0 the time dependent interaction term appears. Then the state will begin to evolve from a pure state into mixed state with an increasing amount of 1st excited state mixed in. Really this approach is only good for a fairly short range of time, from t=0 to about $\gamma t = 0.2$.
Let's see, what can we say about this and what does it seem to show us?
1) Well first maybe we should mention again that the first excited state was selected to be the 2nd energy eigenstate in the mixed state by the "tuning" of the frequency of the oscillating electric field to just the right frequency $2 \pi f = (E_1 - E_o)/\hbar = \omega_1 - \omega_o$.
2) Second, what one calls a quantum jump (from the $E_o$ to $E_1$ state) is not really sudden at all, in our formulation, but rather a continuous evolution of the state due to the influence of the E field.
3) Third, there presumably is a jump at some point. How does that happen? How should we think about that?... Let's take the example of an Mg atom in a photosynthetic molecule. Suppose it starts out in its ground state and an oscillating electric field puts the Mg+ valence electron into a mixed state, as outlined above. The resolution of the energy of the mixed state, in this case and in all cases, is associated with some interaction with the environment outside the atom. In the case of a photosynthetic molecule, the Mg atom is connected to a pretty complex molecular environment via two nitrogen atoms. Once its excited valence electron travels across one of those nitrogen bridges, to begin its photosynthesis journey, the mixed state is over. The probability for the electron to start that journey is related to the coefficient of the 1st excited state in the above mixed state. In that sense one can say that the electron was induced to jump to the excited state and that that was essential to its beginning its travels. Also, the energy lost by the electromagetic field, hf, is equal to the energy gained by the electron.
The resolution of a mixed state, into one energy or the other, tends to involve an interaction between our simple quantum system, which we can model and describe pretty well, and a quite complex environment, which is difficult (or impossible) to model with any precision.
Ideas like wave-function collapse do not have any actual theory behind them. Most physicists in the current era do not believe in anything like that in my experience.
TA excellence in teaching award
There is an excellence in teaching award given to outstanding TAs at UCSC. If anyone would like to write an email about our TA, TJ Torres, and send that to me at zacksc@gmail.com, I would be happy to pass that on at the appropriate time.
Homework #9
Problem #6 is a very important problem (worth putting some time into).
1.
a) Evaluate $L^2 \Psi_{n,l,m,s_z}$ where L is the angular momentum operator.
b) Evaluate $S^2 \Psi_{n,l,m,s_z}$ where S is the spin operator.
c) Evaluate $L_z \Psi_{n,l,m,s_z}$ where L_z is the z component of L.
2. In the first excited states of H, what 4 $\Psi_{n,l,j,j_z}$ eigenstates are made from only one $\Psi_{n,l,m,s_z}$ eigenstate?
3. Before including the spin-orbit and p^4 terms, there are 8 1st excited states, right? How about after? If we group states with the same energy together, are there 2 groups or 3 groups? How many states are in each group?
4. Consider the new 1st excited states*. (*This means only the lowest energy group from the original 8.)
a) How many are there?
b) What are the wave-functions for each (expressed in terms of $\Psi_{n,l,m,s_z}$)?
c) What is the energy of each state in this group in eV?
5. extra credit: How many groups of different energies do the 2nd excited states of H break up into? How many states are in each one and what are their energies?(How many states are there to start with?)
6. In a time varying potential, U(x,t), one can get mixed states whose coefficients depend on time (for example, a 1D harmonic oscillator where, in addition to the $k x^2/2$ static confining potential, you have also a time varying electric field $ E_x cos(2 \pi f t)$).
a) Describe the nature and behavior of the state:
$\Psi(x,t) = (1-\gamma^2 t^2)^{1/2} \Psi_o(x,t) + \gamma t \Psi_1(x,t)$
as a function of time. Assume that $\gamma$ is relatively small. (What are the units of $\gamma$, by the way.)
b) Use sketched graphs and words to describe this evolving state. What is it like at low t? How does it evolve? What does it become?
c) Is there a value of t that should perhaps not be exceeded with this state? Why?
extra credit: d) sketch a rough plot of what the expectation value of x might look like, as a function of t, for an electron in this state.
7. ( Matrix algebra) The vector (1,1) is an eigenvector of the matrix M =
1., c
c , 1.
a) Show that this is true. Determine the eigenvalue associated with (1,1) for c=0.01.
[hint: multiply]
b) What is the other eigenvector of this matrix and what is its eigenvalue (for c=0.01)?
c) is this matrix Hermitian? Are its eigen-vectors orthogonal?
d) is the trace of the matrix equal to the sum of its eigenvalues?
e) Show that the if c=0 then (1,0) and (0,1) are eigenvectors of M. What are their eigenvalues?
Discuss the following: Any non-zero value of c, no matter how small, can really have a big effect on the eigen-vectors of this matrix.
8. On the other hand consider the matrix M2 =
1., c
c , 2.
a) Show that (1,0) and (0,1) are each eigen-vectors of this matrix for c=0 and that they are barely changed at all if c=0.01. Why is that? What is the difference between this matriz and the one in problem 7?



1.
a) Evaluate $L^2 \Psi_{n,l,m,s_z}$ where L is the angular momentum operator.
b) Evaluate $S^2 \Psi_{n,l,m,s_z}$ where S is the spin operator.
c) Evaluate $L_z \Psi_{n,l,m,s_z}$ where L_z is the z component of L.
2. In the first excited states of H, what 4 $\Psi_{n,l,j,j_z}$ eigenstates are made from only one $\Psi_{n,l,m,s_z}$ eigenstate?
3. Before including the spin-orbit and p^4 terms, there are 8 1st excited states, right? How about after? If we group states with the same energy together, are there 2 groups or 3 groups? How many states are in each group?
4. Consider the new 1st excited states*. (*This means only the lowest energy group from the original 8.)
a) How many are there?
b) What are the wave-functions for each (expressed in terms of $\Psi_{n,l,m,s_z}$)?
c) What is the energy of each state in this group in eV?
5. extra credit: How many groups of different energies do the 2nd excited states of H break up into? How many states are in each one and what are their energies?(How many states are there to start with?)
6. In a time varying potential, U(x,t), one can get mixed states whose coefficients depend on time (for example, a 1D harmonic oscillator where, in addition to the $k x^2/2$ static confining potential, you have also a time varying electric field $ E_x cos(2 \pi f t)$).
a) Describe the nature and behavior of the state:
$\Psi(x,t) = (1-\gamma^2 t^2)^{1/2} \Psi_o(x,t) + \gamma t \Psi_1(x,t)$
as a function of time. Assume that $\gamma$ is relatively small. (What are the units of $\gamma$, by the way.)
b) Use sketched graphs and words to describe this evolving state. What is it like at low t? How does it evolve? What does it become?
c) Is there a value of t that should perhaps not be exceeded with this state? Why?
extra credit: d) sketch a rough plot of what the expectation value of x might look like, as a function of t, for an electron in this state.
7. ( Matrix algebra) The vector (1,1) is an eigenvector of the matrix M =
1., c
c , 1.
a) Show that this is true. Determine the eigenvalue associated with (1,1) for c=0.01.
[hint: multiply]
b) What is the other eigenvector of this matrix and what is its eigenvalue (for c=0.01)?
c) is this matrix Hermitian? Are its eigen-vectors orthogonal?
d) is the trace of the matrix equal to the sum of its eigenvalues?
e) Show that the if c=0 then (1,0) and (0,1) are eigenvectors of M. What are their eigenvalues?
Discuss the following: Any non-zero value of c, no matter how small, can really have a big effect on the eigen-vectors of this matrix.
8. On the other hand consider the matrix M2 =
1., c
c , 2.
a) Show that (1,0) and (0,1) are each eigen-vectors of this matrix for c=0 and that they are barely changed at all if c=0.01. Why is that? What is the difference between this matriz and the one in problem 7?



Thursday, February 28, 2013
Spin-Orbit Interaction and its effect of the degeneracy manifolds of hydrogen
The spin-orbit interaction is, at its heart, an interaction between an electron and a proton. However, it is different from the coulomb interaction, $-e^2/r$, in that it depends on the orientation of the spin? What does that mean? What are its consequences? etc. etc.
Those are hard questions. In a way, this is a preview of things that will be covered in Physics 139. One key consequence is that it changes the energies of the states a little bit, of order $10^{-4}$ eV. Equally or more important, it changes the fundamental structure and nature of the degeneracies. Instead of an eightfold degenerate 1st-excited state, one ends up with 6 and 2-fold degeneracies. The eigenstates are specific linear combinations of our "original" eigenstates.
If you get to the end of this and want to see more, maybe post a comment. That will give me some motivation to continue the story.
Here are two more pages. Please feel free to continue the discussion her or in the comments of the HW9 post.


Those are hard questions. In a way, this is a preview of things that will be covered in Physics 139. One key consequence is that it changes the energies of the states a little bit, of order $10^{-4}$ eV. Equally or more important, it changes the fundamental structure and nature of the degeneracies. Instead of an eightfold degenerate 1st-excited state, one ends up with 6 and 2-fold degeneracies. The eigenstates are specific linear combinations of our "original" eigenstates.
If you get to the end of this and want to see more, maybe post a comment. That will give me some motivation to continue the story.
Here are two more pages. Please feel free to continue the discussion her or in the comments of the HW9 post.


Tuesday, February 26, 2013
Cool states.
Monday, February 25, 2013
Wave packet propagation / special project.
This is a post on wave packet propagation, in free space and in a crystal lattice, and a suggestion for a special project if anyone has time for that.
Can you guess what this first giff shows?
(ps. this post contained a number of errors originally. i edited it, hopefully fixing them, on Feb 26.)

A lot of our discussion of electron movement in semiconductors is based on a belief in electron states that are somewhat localized (maybe within 20 lattice sites or therabouts), which maintain their integrity for some bit of time, and can move in a crystal. This belief is based in wave-packet theory. Here is an outline of how one might make some single-electron wave-packet states in free space or in a crystal:
Free space:
In free space we would use the spatial energy eigenstates, $e^{ikx}$ to make the wave packet. (One always has to use the energy eigenstates. In a crystal they are more complex.) In free space they are all of the form $e^{ikx}$ and have energies of $E(k) = \hbar^2 k^2/(2m)$.
A typical wave-packet state is a mixed state made of lots of these energy eigenstates, each with its appropriate time dependence. For example.
$\Psi(x,t) = \int g(k) e^{-ikx} e^{-i \omega(k) t} dk$
where
$g(k) = \sqrt{30/\pi} e^{-30^2 (k-\pi/20)^2}$.
The E vs k relationship:
$E(k) = \hbar^2 k^2/(2m)$,
leads to something like:
$\omega (k) = 1972 (3 \times 10^{18}) k^2/(1.022 \times 10^6)$
where k is in inverse angstroms (and c in there is in angstroms/second.)
For an electron in a crystal the E vs k relationship is different:
$\omega (k) = (E_o - (B/2) cos (kb))/\hbar$
$= (-10/6.6-(2/6.6) cos(k)) \times 10^{16}$
for a crystal with b = 1 Angstrom, B/2 = 2 eV and with $\hbar$ in eV-sec.
(With k in inverse angstroms.)
(Hmmm. It might be better to program with hbar in eV-picoseconds and then have t in picoseconds in the equation for Psi. (Smaller exponents))
Also, the energy eigenstates would be different for an electron in a crystal. (They would be the Bloch states created by a sum over all the lattice sites that we talk about a lot.) I think that at low k, near the bottom of the conduction band, these long wave-length states are pretty similar to free electron states. A bit surprising, but i think it is true.
Anyway, I think what either of those two possibilities will give you is a one-electron wave-packet state that starts out about 10 or 20 lattice spacings (Angstroms) wide and moves to the right as a function of time. The reason I think it moves to the right is that the k values that are used center around k=pi/20, which is positive. I think the packet profile, g(k), is pretty narrow in k; that was my intention.
One could start by just integrating (over k) at t=0 to investigate the nature of $\Psi (x,0)$. The integral is from k = -infinity to infinity.
And then try a small finite t and integrate (k) again to see the difference.
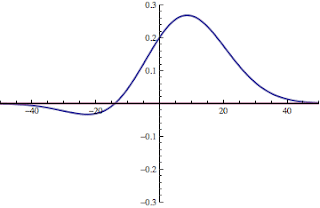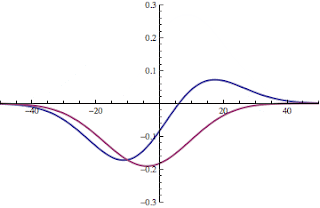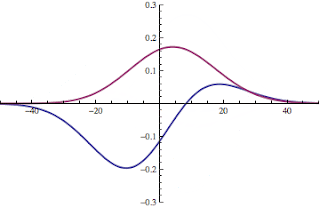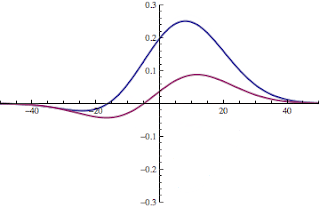
Here is an intriguing result from using a pretty narrow (in k) gaussian "packet" of crystal states centered at k=pi/10.

Can you guess what this first giff shows?
(ps. this post contained a number of errors originally. i edited it, hopefully fixing them, on Feb 26.)

A lot of our discussion of electron movement in semiconductors is based on a belief in electron states that are somewhat localized (maybe within 20 lattice sites or therabouts), which maintain their integrity for some bit of time, and can move in a crystal. This belief is based in wave-packet theory. Here is an outline of how one might make some single-electron wave-packet states in free space or in a crystal:
Free space:
In free space we would use the spatial energy eigenstates, $e^{ikx}$ to make the wave packet. (One always has to use the energy eigenstates. In a crystal they are more complex.) In free space they are all of the form $e^{ikx}$ and have energies of $E(k) = \hbar^2 k^2/(2m)$.
A typical wave-packet state is a mixed state made of lots of these energy eigenstates, each with its appropriate time dependence. For example.
$\Psi(x,t) = \int g(k) e^{-ikx} e^{-i \omega(k) t} dk$
where
$g(k) = \sqrt{30/\pi} e^{-30^2 (k-\pi/20)^2}$.
The E vs k relationship:
$E(k) = \hbar^2 k^2/(2m)$,
leads to something like:
$\omega (k) = 1972 (3 \times 10^{18}) k^2/(1.022 \times 10^6)$
where k is in inverse angstroms (and c in there is in angstroms/second.)
For an electron in a crystal the E vs k relationship is different:
$\omega (k) = (E_o - (B/2) cos (kb))/\hbar$
$= (-10/6.6-(2/6.6) cos(k)) \times 10^{16}$
for a crystal with b = 1 Angstrom, B/2 = 2 eV and with $\hbar$ in eV-sec.
(With k in inverse angstroms.)
(Hmmm. It might be better to program with hbar in eV-picoseconds and then have t in picoseconds in the equation for Psi. (Smaller exponents))
Also, the energy eigenstates would be different for an electron in a crystal. (They would be the Bloch states created by a sum over all the lattice sites that we talk about a lot.) I think that at low k, near the bottom of the conduction band, these long wave-length states are pretty similar to free electron states. A bit surprising, but i think it is true.
Anyway, I think what either of those two possibilities will give you is a one-electron wave-packet state that starts out about 10 or 20 lattice spacings (Angstroms) wide and moves to the right as a function of time. The reason I think it moves to the right is that the k values that are used center around k=pi/20, which is positive. I think the packet profile, g(k), is pretty narrow in k; that was my intention.
One could start by just integrating (over k) at t=0 to investigate the nature of $\Psi (x,0)$. The integral is from k = -infinity to infinity.
And then try a small finite t and integrate (k) again to see the difference.
Here is an intriguing result from using a pretty narrow (in k) gaussian "packet" of crystal states centered at k=pi/10.

Midterm Scores
Below pleased find a sheet with midterm scores with names removed. I would like to tell you that anyone in the class can still get "an A". If you do much better on the final, that will be taken into account so that you can get a grade that reflects your actual understanding. This will not effect anyone else. There is not limit on the number of high grades that can be earned.
One of the main values of a midterm is to prepare you for the final, which will be similar in style and approach. Sometimes having a clear idea what to expect can be very helpful. There will not be any tricks. As in this midterm, I will basically tell you what will be on the test -- what will be asked. It may be useful to look back through the midterm preparation posts and see how they could have helped you more. I think they previewed every problem except 4b and 7 (and even those to some degree).
Since there are some inherent uncertainties in grading, I would like to give everyone a "+5". That is, you actually get a score 5 pts higher than what you see. That takes into account the possibility that you may have been graded too harshly or misunderstood. However, if you want to see about getting more points (regrading), you will be starting from your actual score and working up from there. Does that make sense? This is basically to avoid inadvertently having a system that penalizes people who do not dispute their score. Unless you find something really dramatic, it is often better to spend your
time studying and learning.
------------------
One of the main values of a midterm is to prepare you for the final, which will be similar in style and approach. Sometimes having a clear idea what to expect can be very helpful. There will not be any tricks. As in this midterm, I will basically tell you what will be on the test -- what will be asked. It may be useful to look back through the midterm preparation posts and see how they could have helped you more. I think they previewed every problem except 4b and 7 (and even those to some degree).
Since there are some inherent uncertainties in grading, I would like to give everyone a "+5". That is, you actually get a score 5 pts higher than what you see. That takes into account the possibility that you may have been graded too harshly or misunderstood. However, if you want to see about getting more points (regrading), you will be starting from your actual score and working up from there. Does that make sense? This is basically to avoid inadvertently having a system that penalizes people who do not dispute their score. Unless you find something really dramatic, it is often better to spend your
time studying and learning.
------------------
Sunday, February 24, 2013
PN Junction: initiating recombination and how that leads to light emission.
This video seeks to explain the essential physics of a light emitting diode. A light emitting diode is a p-n junction in which an applied voltage creates a current flow that leads to electrons falling from the conduction band to the valance band, and in the process emitting light (photons). (Each electron that falls emits one photon.)
I think one can understand this physics without getting into the messy details of the "depletion region" at the interface of the p and n-type regions, or the difficult calculations that explain the unusual I-V characteristics of a pn junction. I am interested to get your feedback on how well this works. Do these explanations seem understandable, valid and interesting to you?
I think one can understand this physics without getting into the messy details of the "depletion region" at the interface of the p and n-type regions, or the difficult calculations that explain the unusual I-V characteristics of a pn junction. I am interested to get your feedback on how well this works. Do these explanations seem understandable, valid and interesting to you?
Friday, February 22, 2013
Homework 8:
suggested activities: Watching the videos in the Feb 21 class notes post. Also, it may be helpful to read about moderately doped semiconductors and carrier generation and recombination processes in semiconductors. Also, p-n junctions, but just the most superficial things. I think we can understand them in a simple yet accurate manner. We will focus on p-n junction LEDs, lasers and solar cells.
8. $v= (Bbc/2\hbar c) sin(kb) = (Bbc/2\hbar c) (\pi/20)$
= (4 eV 1 A/(2 1972 eV-A)) (pi/20) c
= 4.8x10^6 cm/sec


9. One more problem! (the focus of this problem is to help you build your skills of actually calculating numbers.)
Consider an electron in the conduction band of a crystal for which the energy is given by:
$E_c (k) = E_o - (B/2) cos (kb)$.
Then confirm that,
$v(k) = (Bb/2 \hbar) sin(bk)$,
and, for the case b = 1 angstrom and B=4 eV,
a) calculate v(k) at $k = \pi /(20 b)$ in Angstoms per second and in cm/sec. Get numbers! (Soon we may try to show (numerically) that this is the electron speed associated with this state.)
Due Friday, 3 PM
8. $v= (Bbc/2\hbar c) sin(kb) = (Bbc/2\hbar c) (\pi/20)$
= (4 eV 1 A/(2 1972 eV-A)) (pi/20) c
= 4.8x10^6 cm/sec


9. One more problem! (the focus of this problem is to help you build your skills of actually calculating numbers.)
Consider an electron in the conduction band of a crystal for which the energy is given by:
$E_c (k) = E_o - (B/2) cos (kb)$.
Then confirm that,
$v(k) = (Bb/2 \hbar) sin(bk)$,
and, for the case b = 1 angstrom and B=4 eV,
a) calculate v(k) at $k = \pi /(20 b)$ in Angstoms per second and in cm/sec. Get numbers! (Soon we may try to show (numerically) that this is the electron speed associated with this state.)
Due Friday, 3 PM
1. a) If a semiconductor has a band gap of 1 eV what frequency of photon would you require in order to create an electron-hole-pair excitation? What color is that?
b) What color of photon would a semiconductor with a 1.9 eV band gap emit in a transition from the bottom of the conduction band to the top of the valence band?
2. Suppose you have a 1-dimensional semiconductor that is 2 cm long. Suppose the left half is doped with 10^4 acceptors per cm and the right half is doped with 10^4 donors per cm.
a) graph the density of electrons in the conduction band and the density of holes in the valence band (empty states) as a function of x. You can call the density of electrons in the conduction band, n, and the density of holes in the valence band, p.
(hint: don't make this too complicated. It is really simple!)
(hint: don't make this too complicated. It is really simple!)
3. Consider a 1D semiconductor, our typical one, with a band gap of 0.5 eV between the top of the valence band and the bottom of the conduction band. Suppose you substitution dope the right-hand half of it with 10^4 donor atoms per cm and then apply a voltage (electron field) that pushes the mobile electrons in the conduction band (on the right) toward the left, into an region where they all fall into the valence band with each one emitting a photon. Let's assume that, in response to the applied voltage, the electrons move with a speed of 3 $10^6$ cm/sec.
a1) sketch a picture of that...
a1) sketch a picture of that...
a2) Would the region on the left where the downward transition takes place need to be doped at all? why or why not? In what way would you dope it to allow downward "recombination" transitions.
b) How many photons would be emitted per second?
c) what would be the energy of each photon (more or less)?
d) how much total power would be emitted? (in eV/sec, and Joules/sec = Watts)
4. Now consider a 3D semiconductor with a band gap of 0.5 eV and doped on the right-hand half of it with 10^17 donors/cm^3. Apply a voltage (electron field) that pushes those electrons toward the left (at a speed of 3 $10^6$ cm/sec) into a region on the left where they all fall into the valence band with each one emitting a photon.
a) would the region on the left need to be doped? In what way? Why?
b) How many photons would be emitted per second? (are the units the same or different than in #3? Why?)
c) what would be the energy of each photon (more or less)?
d) how much total power would be emitted? (what are the units of that?)
5. a) What semiconductor band gap would be best suited to creating a red LED?
b) a) What semiconductor band gap would be best suited to creating a green LED?
6. Discuss how substituting N in GaAs might possibly help you obtain a green LED (i.e., help you change a red LED material into a green one?)
7. Consider a 1D semiconductor with an energy gap of 0.8 eV. Suppose the density of states near the bottom of the conduction band is g(E) = $2 \times 10^9$ states/(eV-cm). Further, suppose we treat g(E) as constant within the band and zero in the band gap).
a) sketch a plot of this approximate g(E) (which is either zero or $2 \times 10^9$ states/(eV-cm)).
b) Integrate the product g(E) times f(E) over the range of the conduction band, where f(E) is the Fermi function. Put the Fermi energy $E_F$ right in the middle of the gap and set KT=0.025 eV = 1/40 eV.
(important hints:
hint 1) What is the largest value of f(E) for E in the range of the conduction band? If it is small, then you can ignore the +1 in the denominator and the integrand becomes much easier. Perhaps if you are lucky the integrad becomes a constant, g(E), times a simple decaying exponential? (Do you feel lucky?)
hint 2) The upper limit of integration (from the top of the conduction band) will give you a very, very, very small number. I would suggest that you totally ignore it.)
c) What are the units of your result from b)?
What is the numerical value of your result? (Do you need to have anything else given?)
(important hints:
hint 1) What is the largest value of f(E) for E in the range of the conduction band? If it is small, then you can ignore the +1 in the denominator and the integrand becomes much easier. Perhaps if you are lucky the integrad becomes a constant, g(E), times a simple decaying exponential? (Do you feel lucky?)
hint 2) The upper limit of integration (from the top of the conduction band) will give you a very, very, very small number. I would suggest that you totally ignore it.)
c) What are the units of your result from b)?
What is the numerical value of your result? (Do you need to have anything else given?)
d) Explain why this calculation might give you the density of electrons in the conduction band at room temperature for this semiconductor when it is un-doped (intrinsic).
8. a) What is the relationship between the structure of diamond and the structure of Silicon?
b) Comparing the C-C bond in Diamond, and the C-C bond in Graphene: which is strongest? Why do you think that might be?
Appendix:
The Fermi function is:
$f(E) = (e^{(E-E_F)/KT} + 1)^{-1}$.
It tells you the probability, in a thermal physics/statistical physics sense, that a particular state at energy E is occupied. Note that it can't be bigger than 1 (Fermions) or less than zero.
You are given that KT= .025 eV (so you don't need to know K) and also where $E_F$ is (in the center of the gap). Note that whenever $E-E_F$ is greater than about 3KT you can approximate f(E) by a simple exponential.
8. a) What is the relationship between the structure of diamond and the structure of Silicon?
b) Comparing the C-C bond in Diamond, and the C-C bond in Graphene: which is strongest? Why do you think that might be?
Appendix:
The Fermi function is:
$f(E) = (e^{(E-E_F)/KT} + 1)^{-1}$.
It tells you the probability, in a thermal physics/statistical physics sense, that a particular state at energy E is occupied. Note that it can't be bigger than 1 (Fermions) or less than zero.
You are given that KT= .025 eV (so you don't need to know K) and also where $E_F$ is (in the center of the gap). Note that whenever $E-E_F$ is greater than about 3KT you can approximate f(E) by a simple exponential.
Student researcher position available.
I am looking for an undergraduate student to work next year as a research assistant on a project in which we calculate electron states in unusual materials. These will tend to be materials that have interesting quantum physics characteristics and possible potential for future device applications. Examples include topological insulators.
The calculations are doing using a LINUX based program called FPLO (full potential, local orbitals), which you can check out online, so some expertise with LINUX type computing would be ideal. The program is all up and working, but it is not easy (for me) to run. (The undergrad setting it up now seems to do just fine, however.) I hope/expect to have funding to pay for about 160 hours or maybe more, i.e., about 20 weeks at 8 hours per week. This would likely involve a close collaboration with Arthur Ramirez, a physicist from Bell Labs who is now Dean of Engineering at UCSC, who is interested in these materials and does experiments on them.
If interested, please email me at zacksc@gmail.com
Feb 21 Class Notes and Videos.
This post will contain videos and other content related to our Feb 21 class. Specifically:
I tried to make a 3rd video dealing with hole doping and the very interesting and subtle question of how a few empty states in the valence band behave as if they were mobile positively charged "electron-like" carriers. These are created by doping with "acceptor" atoms, atoms that need one more electron to meet their bonding-related obligations. Anyway, the sound didn't work, but here is the tiff from that.

1) A video describing how one creates and uses a model of a 1-dimensional metal. Starting with a 1D atom with a single electron (in the ground state), this model brings many atoms together to create the simplest approach to modeling a metal that I know of. In general, a metal must have a partially filled band; this one has a half-filled band. (A lot of cool physics is associated with systems with a half-filled band (or a very nearly half-filled band. High temperature superconductors, Mott insulators, Peierls instabilities...) But we will use the half-filled band to help us understand the basic nature of a metal, which is that it has a boundary where the states go from being occupied to being unoccupied -- rather abruptly! This is associated with Enrico Fermi and called the Fermi edge or Fermi surface and there is a specific k and energy where that occurs, $k_F$, $E_F$. Conductivity, current flow, in the presence of an electric arises from a shifting of the boundary. The electric field breaks the symmetry (of left and right being equivalent), shifts the boundary to one side, and then there is a net current associated with the uncompensated electrons.
The second video introduces a 1D model of a semiconductor. This is necessarily more complex because a semiconductor must have 2 bands: one that is fully occupied and one that is empty (to begin with). The occupied one is called the valence band; the empty one is called the conduction band. One of the goals of semiconductor physics is to find a way to get some electrons into the empty conduction band. This video presents the model and discusses how to do that (get electrons in the CB) by doping. That is, by substituting an atom with an extra electron at a few random points in the lattice with the hope that that extra electron will escape into the conduction band.
The second video introduces a 1D model of a semiconductor. This is necessarily more complex because a semiconductor must have 2 bands: one that is fully occupied and one that is empty (to begin with). The occupied one is called the valence band; the empty one is called the conduction band. One of the goals of semiconductor physics is to find a way to get some electrons into the empty conduction band. This video presents the model and discusses how to do that (get electrons in the CB) by doping. That is, by substituting an atom with an extra electron at a few random points in the lattice with the hope that that extra electron will escape into the conduction band.
I tried to make a 3rd video dealing with hole doping and the very interesting and subtle question of how a few empty states in the valence band behave as if they were mobile positively charged "electron-like" carriers. These are created by doping with "acceptor" atoms, atoms that need one more electron to meet their bonding-related obligations. Anyway, the sound didn't work, but here is the tiff from that.
Wednesday, February 20, 2013
Preparation for Thursday's Class.
As things get more complex and interwoven, it becomes even more important (critical even) to prepare before each class (for you, that is). Mostly that involves spending some time (1/2 hour, an hour, 4 hours...) looking critically at what we did in the previous class and thinking about what could come next. For example, coming into tomorrow's class you would be helped by going over: the expressions for crystal states, the energy of crystal states, the velocity of crystal states, how these things depend on k, the units of k... Thinking about those things, what they are, etc., will be essential to following what we will do for the next 3 classes or so, which will lead to an understanding of a pn junction LED, LASER and solar cell.
The homework for this week is a good place to find the relevant equations, relations and problems related to Thursday's class.
===========================
These are some very rough notes related to future classes. I don't think they are very helpful but i put them here just in case i am wrong about that:


The homework for this week is a good place to find the relevant equations, relations and problems related to Thursday's class.
===========================
These are some very rough notes related to future classes. I don't think they are very helpful but i put them here just in case i am wrong about that:


Tuesday, February 19, 2013
Homework 7: electrons in metals
This homework gives you a chance to explore electrons in metals, current flow and things like that. It will stay at a pretty high-level: we start with an expression for energy vs k, which we have discussed and tried to justify to some degree. We also take as "given", a straight-forward, easy to use relationship for velocity. Our metal is one-dimensional (1D) with a particular electron density, $10^8$ electrons/cm and a particular filling of the band (1/2 filled).
$E_k = E_o -(B/2) cos (bk)$, where B is in eV and typically around 1 to 8 eV.
$v_k = (1/\hbar) \partial{E_k}/\partial{k}$
1. Consider a metal with one well per 0.1 nm ($b = 0.1 nm$) and one (itinerant=non-local) electron per well. That leads to an electron density of 1 electron per 0.1 nm, or, equivalently, $10^8$ electrons/cm, right? With one electron per well we will get, i think, a half-filled band, that is, all the states between $k = -\pi/2b$ and $k = \pi/2b$ are filled. Assume that B = 4 eV.
a) Sketch $E_k$ vs k and indicate on your sketch where the boundary between filled and empty states is.
b) What is the speed of an electron in a boundary state, i.e., the state $\psi_k$ with $k = \pi/2b$ (also known as $k_f$). What is it in cm/sec? (feel free to post here for a quick check and comparison with others)
c) When there are an equal number of electrons in k and -k states, the net current is zero. However, an electric field can skew the occupation boundaries so that that balance is disrupted. Suppose that the balance is skewed so that 1 in 1000 right-moving electrons are uncompensated. What is the net current carried by these electrons. [Hint: You can assume all of them have essentially the same speed and use the equation I=nev to calculate the current in electrons per second or in coulombs per second. Here n is the density of current carrying, uncompensated electrons (in electrons per cm), e is the charge of an electron, and v is the speed (from b). Do you get a current more or less in the micro-ampere range. What is it?
2. Compare the speed of the electron in problem 7 of the midterm, to the speed of an electron in the "band state" $\psi_k$, with $k=\pi/2b$ with B = 1 eV. Are they similar at all? Feel free to comment/discuss here. (Your first line could be: "how do we define the speed of the electron in problem 7?")
3. What is the nature of the time dependence of the crystal state:
$\psi_{o,k} (x,t) = \sum^\infty_{n= -\infty} e^{inkb} \psi_o (x-nb)$.
Is this an eigenstate or a mixed state?
Please ask questions about this, comment or share your thoughts below...
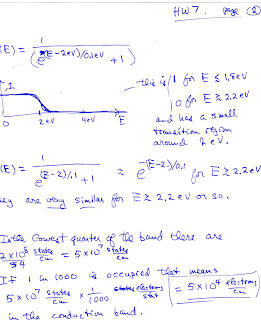
4. Graph the function $f(E) = 1/(e^{(E-2)/.1} + 1)$ from about zero to 5. Describe it.
5. Compare the functions $f(E) = 1/(e^{(E-2)/.1} + 1)$ and $f(E) = e^{-(E-2)/.1}$. Where are most different? Are they similar over any region? Why?
6. A conduction band of a semi-conductor can be just like that of a metal in terms of the nature of the states $\psi_k$ and the E vs k relation, but it is completely different in terms of the occupation of the states. Typically in a semi-conductor only some states near the bottom of the conduction band are occupied at all.
a) Suppose 1 in 1000 of the states in the lowest quarter of the band (between $k = -\pi/4b$ and $\pi/4b$) are occupied and the rest of the conduction band is empty. How many electrons/cm is that in the conduction band? (units are electrons/cm)
Appendix:
This energy vs k relation (called a "dispersion relation"),
$E_k = E_o -(B/2) cos (bk)$,
refers to the energies of states of the form:
$\psi_{o,k} (x) = \sum^\infty_{n= -\infty} e^{inkb} \psi_o (x-nb))$.
These are the states made of "combinations of atomic orbitals", as we discussed and sketched last week.
Although it is not at all obvious, once you put in their time dependence (see problem 4), these states have a velocity given by the equation:
$v_k = (1/\hbar) \partial{E_k}/\partial{k}$
(which you might notice is proportional to k at low kb just like for free electron states.)
Oh, by the way, a note on terminology:
1) the "height" of the band, which is B since the band goes from a lowest energy of $E_o - B/2$ to a maximum energy of $E_o + B/2$ (at $k=\pi/b$, is generally called "bandwidth".
What looks like it should be called width, the interval from $-\pi/b$ to $\pi/b$, is called the Brillouin zone (or sometimes 1st Brillouin zone). The points $-\pi/b$ to $\pi/b$ are called the "Brillouin zone edge."
Solution notes:
$E_k = E_o -(B/2) cos (bk)$, where B is in eV and typically around 1 to 8 eV.
$v_k = (1/\hbar) \partial{E_k}/\partial{k}$
1. Consider a metal with one well per 0.1 nm ($b = 0.1 nm$) and one (itinerant=non-local) electron per well. That leads to an electron density of 1 electron per 0.1 nm, or, equivalently, $10^8$ electrons/cm, right? With one electron per well we will get, i think, a half-filled band, that is, all the states between $k = -\pi/2b$ and $k = \pi/2b$ are filled. Assume that B = 4 eV.
a) Sketch $E_k$ vs k and indicate on your sketch where the boundary between filled and empty states is.
b) What is the speed of an electron in a boundary state, i.e., the state $\psi_k$ with $k = \pi/2b$ (also known as $k_f$). What is it in cm/sec? (feel free to post here for a quick check and comparison with others)
c) When there are an equal number of electrons in k and -k states, the net current is zero. However, an electric field can skew the occupation boundaries so that that balance is disrupted. Suppose that the balance is skewed so that 1 in 1000 right-moving electrons are uncompensated. What is the net current carried by these electrons. [Hint: You can assume all of them have essentially the same speed and use the equation I=nev to calculate the current in electrons per second or in coulombs per second. Here n is the density of current carrying, uncompensated electrons (in electrons per cm), e is the charge of an electron, and v is the speed (from b). Do you get a current more or less in the micro-ampere range. What is it?
2. Compare the speed of the electron in problem 7 of the midterm, to the speed of an electron in the "band state" $\psi_k$, with $k=\pi/2b$ with B = 1 eV. Are they similar at all? Feel free to comment/discuss here. (Your first line could be: "how do we define the speed of the electron in problem 7?")
3. What is the nature of the time dependence of the crystal state:
$\psi_{o,k} (x,t) = \sum^\infty_{n= -\infty} e^{inkb} \psi_o (x-nb)$.
Is this an eigenstate or a mixed state?
Please ask questions about this, comment or share your thoughts below...
4. Graph the function $f(E) = 1/(e^{(E-2)/.1} + 1)$ from about zero to 5. Describe it.
5. Compare the functions $f(E) = 1/(e^{(E-2)/.1} + 1)$ and $f(E) = e^{-(E-2)/.1}$. Where are most different? Are they similar over any region? Why?
6. A conduction band of a semi-conductor can be just like that of a metal in terms of the nature of the states $\psi_k$ and the E vs k relation, but it is completely different in terms of the occupation of the states. Typically in a semi-conductor only some states near the bottom of the conduction band are occupied at all.
a) Suppose 1 in 1000 of the states in the lowest quarter of the band (between $k = -\pi/4b$ and $\pi/4b$) are occupied and the rest of the conduction band is empty. How many electrons/cm is that in the conduction band? (units are electrons/cm)
Appendix:
This energy vs k relation (called a "dispersion relation"),
$E_k = E_o -(B/2) cos (bk)$,
refers to the energies of states of the form:
$\psi_{o,k} (x) = \sum^\infty_{n= -\infty} e^{inkb} \psi_o (x-nb))$.
These are the states made of "combinations of atomic orbitals", as we discussed and sketched last week.
Although it is not at all obvious, once you put in their time dependence (see problem 4), these states have a velocity given by the equation:
$v_k = (1/\hbar) \partial{E_k}/\partial{k}$
(which you might notice is proportional to k at low kb just like for free electron states.)
Oh, by the way, a note on terminology:
1) the "height" of the band, which is B since the band goes from a lowest energy of $E_o - B/2$ to a maximum energy of $E_o + B/2$ (at $k=\pi/b$, is generally called "bandwidth".
What looks like it should be called width, the interval from $-\pi/b$ to $\pi/b$, is called the Brillouin zone (or sometimes 1st Brillouin zone). The points $-\pi/b$ to $\pi/b$ are called the "Brillouin zone edge."
Solution notes:
Saturday, February 16, 2013
Midterm tips & solution notes (Feb 23)
Midterm tip -1: Please occupy only every other seat starting with the seat closest to the aisle.
Midterm tips 0: Plan to stay for the entire 1:45 minutes. With more time you can do more. Questions 5-7 are somewhat open-ended and you are invited to "go deep" on those. More thought, more nuance, in your responses is better. Additionally, sitting and concentrating for the whole time will help build your stamina for your 3 hour finals.
Problems1-4 are a total of 40 pts (8, 8, 10, 14)
Problems 5-7 are 20 pts each (expect to spend a lot of time on these).
8 is extra credit (about another 20 pts or so, also time consuming)
PS. In my opinion, adequate sleep, even a late morning nap, is helpful, especially when you will be ask to think and make connections.
Midterm tip #1: Include a graph!
Whenever you are asked to write a paragraph about something, or to discuss or explain something: include a graph! (or more than one graph if appropriate.) The graphs should, of course, be relevant and they should be referred to in your discussion. Labels on the axes are usually a good idea. Graphs and the discussion that accompanies them are an excellent way to get full credit and even extra credit. Even when you are not explicitly ask for a graph, please do include relevant graphs.
Midterm tip #2: Ignore extraneous information.
Sometimes you will be given extraneous information, information you do not need. That is to see if you can ferret out what is really important and essential to solve a particular problem. You are advised to trust your knowledge and preparation, and ignore extraneous information when the need arises.
Midterm tip #3: It helps if we all use the same states to start with. (The same notation.) For example, what I have for the 1DHO is:
$\psi_o (x) = (1/a \sqrt{\pi})^{1/2}e^{-x^2/(2a^2)}$
$\psi_1 (x) = (2/a \sqrt{\pi})^{1/2}(x/a)e^{-x^2/(2a^2)}$
$\psi_2 (x) = (2/a \sqrt{\pi})^{1/2}((x/a)^2-1/2)e^{-x^2/(2a^2)}$
Does that agree with what everyone else has and has been using? (These are discussed in an ancient video (from a December post, i think; the 2nd video made for this class) along with the corresponding infinite sq well states.)
Also, for the infinite square well centered at x=0, as requested below, i think the states are:
$\psi_o (x) = (2/L)^{1/2}cos (\pi x /L)$
$\psi_1 (x) = (2/L)^{1/2}sin (2 \pi x /L)$
$\psi_2 (x) = (2/L)^{1/2}cos (3 \pi x /L)$
================================
Solution notes for the midterm problems:





Midterm tips 0: Plan to stay for the entire 1:45 minutes. With more time you can do more. Questions 5-7 are somewhat open-ended and you are invited to "go deep" on those. More thought, more nuance, in your responses is better. Additionally, sitting and concentrating for the whole time will help build your stamina for your 3 hour finals.
Problems1-4 are a total of 40 pts (8, 8, 10, 14)
Problems 5-7 are 20 pts each (expect to spend a lot of time on these).
8 is extra credit (about another 20 pts or so, also time consuming)
PS. In my opinion, adequate sleep, even a late morning nap, is helpful, especially when you will be ask to think and make connections.
Midterm tip #1: Include a graph!
Whenever you are asked to write a paragraph about something, or to discuss or explain something: include a graph! (or more than one graph if appropriate.) The graphs should, of course, be relevant and they should be referred to in your discussion. Labels on the axes are usually a good idea. Graphs and the discussion that accompanies them are an excellent way to get full credit and even extra credit. Even when you are not explicitly ask for a graph, please do include relevant graphs.
Midterm tip #2: Ignore extraneous information.
Sometimes you will be given extraneous information, information you do not need. That is to see if you can ferret out what is really important and essential to solve a particular problem. You are advised to trust your knowledge and preparation, and ignore extraneous information when the need arises.
Midterm tip #3: It helps if we all use the same states to start with. (The same notation.) For example, what I have for the 1DHO is:
$\psi_o (x) = (1/a \sqrt{\pi})^{1/2}e^{-x^2/(2a^2)}$
$\psi_1 (x) = (2/a \sqrt{\pi})^{1/2}(x/a)e^{-x^2/(2a^2)}$
$\psi_2 (x) = (2/a \sqrt{\pi})^{1/2}((x/a)^2-1/2)e^{-x^2/(2a^2)}$
Does that agree with what everyone else has and has been using? (These are discussed in an ancient video (from a December post, i think; the 2nd video made for this class) along with the corresponding infinite sq well states.)
Also, for the infinite square well centered at x=0, as requested below, i think the states are:
$\psi_o (x) = (2/L)^{1/2}cos (\pi x /L)$
$\psi_1 (x) = (2/L)^{1/2}sin (2 \pi x /L)$
$\psi_2 (x) = (2/L)^{1/2}cos (3 \pi x /L)$
================================
Solution notes for the midterm problems:





Friday, February 15, 2013
Homework 6 solutions and discussion.

 Homework 6 deals with the one-electron states of multiple-well systems. We start with two wells (1 and 2), and look at a 4-well potential in problem 3. The (spatial) wave-functions for these multiple-well systems (system meaning both an electron and the potential), is constructed in our approach by combining atom-like wave-functions centered at different places along the x axis. Each added node increases the energy slightly as discussed in problem 3. The states are orthogonal. These states are not exactly correct, but they give us a good idea what the exact states would look like and how their energies would be juxtaposed.
Homework 6 deals with the one-electron states of multiple-well systems. We start with two wells (1 and 2), and look at a 4-well potential in problem 3. The (spatial) wave-functions for these multiple-well systems (system meaning both an electron and the potential), is constructed in our approach by combining atom-like wave-functions centered at different places along the x axis. Each added node increases the energy slightly as discussed in problem 3. The states are orthogonal. These states are not exactly correct, but they give us a good idea what the exact states would look like and how their energies would be juxtaposed.Problem 4 is a big problem and will guide our study of electron states (wave-functions) in crystals, including metals and semiconductors. I'll post more on that here later.
Midterm Review special Section: Monday 4 PM
Our TA, TJ Torres, has agreed to do a special review-for-the-midterm section on Monday from 4- 5 PM. The details of where and when and how to get into the building are as follows:
(from TJ Torres) "Last night at my section there was significant interest in my
hosting a midterm review, so I committed to doing so from 4-5pm on
Monday in the normal section location (ISB 231). I know school is closed, but I
will just let people in, checking the courtyard ISB entrance at 4 and
4:05."
(from TJ Torres) "Last night at my section there was significant interest in my
hosting a midterm review, so I committed to doing so from 4-5pm on
Monday in the normal section location (ISB 231). I know school is closed, but I
will just let people in, checking the courtyard ISB entrance at 4 and
4:05."
Wednesday, February 13, 2013
Another midterm preparation post.
(edited on Weds evening, Feb 13)
The midterm is on Feb 19 (as posted and announced previously).
You can bring a one page sheet. Suggestions regarding what to put on it are here, and in the earlier posts on midterm preparation. This is the third in a series of 3 midterm preparation related posts which include:
i) Midterm, Feb 19: midterm preparation; Quiz. (posted Jan 31)
ii) Quiz: a quiz is now posted here. (posted Feb 1)
-this quiz, if you take it as suggested, is a good way to test your preparation. If you just read it before preparing that is not as useful as using it to simulate a real quiz and thereby testing your equation sheet and your readiness for your midterm. In addition to the quiz, there is discussion of the midterm in this post as well.
Suggestions regarding how to prepare and what to include on your equation sheet ( and not include) are in those older posts as well.
In general, I think reading and understanding most things on the course blog would be good preparation. The older posts are not gone. They will appear when you click "older posts" at the bottom of the page.
Specific tips:
This is quantum. hbar is important. so is m, the mass of an electron. Have hbar and hbar c ready in various unit systems. We like eV for energy. hbar c is often much preferable to work with. Know c in m/s, cm/s, nm/s and A/s. know mc^2 for an electron in Ev. Of course you can write all these on your equation sheet.
We do expectation value calculations. Have some extensive, but not insane, integral tables prepared. Use Wolfram Alpha to create them. Definite integrals.
Understand x, p, x^2, confinement and kinetic energy and potential energy. Be ready to calculate, graph and explain anything related to those things.
Understand the origin of the size of the hydrogen atom.
Understand how to quickly calculate energies, especially kinetic energy, in eV.
Be prepared to illustrate states in both 1D, for the HO and square well, and in 3D, for the hydrogen atom. Understand how to use contour plots and plots along a particular axis to illustrate the nature of a state. Be able to illustrate any 1st-excited state as well as the ground state and to discuss their nature. That includes all sp2 states. (Though don't get too carried away with the details of sp2 contours. I will not asked you to draw an sp2 state contour.)
Be prepared to sketch integrands, including KE integrands.
Be prepared to sketch states and integrands for double wells.
Be prepared to calculate time-dependent expectation values.
In some problems you will be given information you do not need. This is to test if you really understand quantum physics (rather than just having a developed skill related to how to guess what professors want you to with whatever information you are given.). If you understand something don't be fooled by extraneous information. Trust your preparation, knowledge and intuition.
The midterm is on Feb 19 (as posted and announced previously).
You can bring a one page sheet. Suggestions regarding what to put on it are here, and in the earlier posts on midterm preparation. This is the third in a series of 3 midterm preparation related posts which include:
i) Midterm, Feb 19: midterm preparation; Quiz. (posted Jan 31)
ii) Quiz: a quiz is now posted here. (posted Feb 1)
-this quiz, if you take it as suggested, is a good way to test your preparation. If you just read it before preparing that is not as useful as using it to simulate a real quiz and thereby testing your equation sheet and your readiness for your midterm. In addition to the quiz, there is discussion of the midterm in this post as well.
Suggestions regarding how to prepare and what to include on your equation sheet ( and not include) are in those older posts as well.
In general, I think reading and understanding most things on the course blog would be good preparation. The older posts are not gone. They will appear when you click "older posts" at the bottom of the page.
Specific tips:
This is quantum. hbar is important. so is m, the mass of an electron. Have hbar and hbar c ready in various unit systems. We like eV for energy. hbar c is often much preferable to work with. Know c in m/s, cm/s, nm/s and A/s. know mc^2 for an electron in Ev. Of course you can write all these on your equation sheet.
We do expectation value calculations. Have some extensive, but not insane, integral tables prepared. Use Wolfram Alpha to create them. Definite integrals.
Understand x, p, x^2, confinement and kinetic energy and potential energy. Be ready to calculate, graph and explain anything related to those things.
Understand the origin of the size of the hydrogen atom.
Understand how to quickly calculate energies, especially kinetic energy, in eV.
Be prepared to illustrate states in both 1D, for the HO and square well, and in 3D, for the hydrogen atom. Understand how to use contour plots and plots along a particular axis to illustrate the nature of a state. Be able to illustrate any 1st-excited state as well as the ground state and to discuss their nature. That includes all sp2 states. (Though don't get too carried away with the details of sp2 contours. I will not asked you to draw an sp2 state contour.)
Be prepared to sketch integrands, including KE integrands.
Be prepared to sketch states and integrands for double wells.
Be prepared to calculate time-dependent expectation values.
In some problems you will be given information you do not need. This is to test if you really understand quantum physics (rather than just having a developed skill related to how to guess what professors want you to with whatever information you are given.). If you understand something don't be fooled by extraneous information. Trust your preparation, knowledge and intuition.
Monday, February 11, 2013
Topical Outline and notes.
Below is a topical outline covering at least the next few weeks, and below that some notes related to the outline (filling in some selected details and nuances.)
So far we have covered:
*1D quantum wave-functions, with an emphasis on spatial wave-functions, but looking also at energies and time-dependence in missed states. *2 and 3D quantum wave-functions: with an emphasis on degeneracy and combining degenerate states to get novel and important spatial wave-functions, e.g., sp2 *Periodic table: with an emphasis on sp hybridization and the 2nd row. *Energy in quantum physics: with an emphasis on quantum kinetic energy and its relationship to confinement. (In most of the above, expectation value calculations have played a significant role in our understanding.) ------
Topical Outline:
*States in molecules
*States in crystals *
Bands of states (including mention of velocity of packets formed from band states)
Filling of band states
Metals Fermi function, Fermi energy
Electric field and conductivity. ( a few electrons moving really fast)
*Semiconductors:
Valence and conduction bands
Electrons and holes carriers from optical excitation, temperature and doping.
p-n junction LEDs, LASERs and solar cells
Spectroscopy:
H atom
length scales of light and the atom
inducing mixed states (E field)
fine structure, spin-orbit coupling
Notes: States of molecules and crystals: we will explore how to use wave-functions from our study of atoms to create wave-functions appropriate for molecules and crystals. Using energy bands in one-dimensional crystals as a starting point and a reference point we will examine the origin of energy bands in crystals and examine the states that belong to a particular band. Look at how they are formed and in what ways they are similar to each other and in what ways they are different. This will allow is to explore the natures of metals, semiconductors and insulators, as well as things like electrical conductivity and optical transitions in metals, semiconductors and insulators. We will see how the color of copper and gold can be connected to the Schrodinger equation. Fermi statistics in metals and semiconductors: We will see how metals have a Fermi surface with very energetic electrons, and how current in a metal involves a few very-fast moving electrons (fewer electrons than you might expect, each moving faster than expected). In semiconductors we will delineate the valence and conduction bands, and talk about optically created carriers (photoconductivity), as well as finite temperature and doping. Then p-n junctions and p-n junction lasers, leds and solar cells.
Difficulties of solving and understanding systems with many interacting electrons. Limits on using the Schrodinger equation to understand complex or strongly interacting systems. More is different is an important concept that helps define what is important and challenging in physics and the difficulties of going further than we have with the Schrodinger equation or any reductionist approach.
Back to the hydrogen atom, we will look at spin-orbit splitting (which is part of what is called fine structure). In this we see the importance of a new interaction term in producing new results and physics. We will revisit spin and consider its obtuse relationship to angular momentum. This will include another look at atomic spectroscopy and the $\psi_{n,l,m}$ states.
So far we have covered:
*1D quantum wave-functions, with an emphasis on spatial wave-functions, but looking also at energies and time-dependence in missed states. *2 and 3D quantum wave-functions: with an emphasis on degeneracy and combining degenerate states to get novel and important spatial wave-functions, e.g., sp2 *Periodic table: with an emphasis on sp hybridization and the 2nd row. *Energy in quantum physics: with an emphasis on quantum kinetic energy and its relationship to confinement. (In most of the above, expectation value calculations have played a significant role in our understanding.) ------
Topical Outline:
*States in molecules
*States in crystals *
Bands of states (including mention of velocity of packets formed from band states)
Filling of band states
Metals Fermi function, Fermi energy
Electric field and conductivity. ( a few electrons moving really fast)
*Semiconductors:
Valence and conduction bands
Electrons and holes carriers from optical excitation, temperature and doping.
p-n junction LEDs, LASERs and solar cells
Spectroscopy:
H atom
length scales of light and the atom
inducing mixed states (E field)
fine structure, spin-orbit coupling
Notes: States of molecules and crystals: we will explore how to use wave-functions from our study of atoms to create wave-functions appropriate for molecules and crystals. Using energy bands in one-dimensional crystals as a starting point and a reference point we will examine the origin of energy bands in crystals and examine the states that belong to a particular band. Look at how they are formed and in what ways they are similar to each other and in what ways they are different. This will allow is to explore the natures of metals, semiconductors and insulators, as well as things like electrical conductivity and optical transitions in metals, semiconductors and insulators. We will see how the color of copper and gold can be connected to the Schrodinger equation. Fermi statistics in metals and semiconductors: We will see how metals have a Fermi surface with very energetic electrons, and how current in a metal involves a few very-fast moving electrons (fewer electrons than you might expect, each moving faster than expected). In semiconductors we will delineate the valence and conduction bands, and talk about optically created carriers (photoconductivity), as well as finite temperature and doping. Then p-n junctions and p-n junction lasers, leds and solar cells.
Difficulties of solving and understanding systems with many interacting electrons. Limits on using the Schrodinger equation to understand complex or strongly interacting systems. More is different is an important concept that helps define what is important and challenging in physics and the difficulties of going further than we have with the Schrodinger equation or any reductionist approach.
Back to the hydrogen atom, we will look at spin-orbit splitting (which is part of what is called fine structure). In this we see the importance of a new interaction term in producing new results and physics. We will revisit spin and consider its obtuse relationship to angular momentum. This will include another look at atomic spectroscopy and the $\psi_{n,l,m}$ states.
HW 5 solutions.
Enclosed are HW 5 solutions. Problems 1-3 provide an opportunity to understand confinement and its consequences. $\Delta x$ reflects the value of x^2, not x, in our problems; this is a measure of confinement. Similarly, $\Delta p$ reflects the value of p^2, not p, and is proportional to kinetic energy. Thus it is natural and probably less subject to misinterpretation to recast the "uncertainty" relationship, as we did, as a relationship between confinement and kinetic energy.
I believe that some people found problem 4 to be a little tricky or confusing. My approach to problem 4 is on the last page. For the HO GS you start with kinetic energy as a function of a. And we also have a relationship between a and $\Delta x$. You can use that to substitute out a and get a relationship between T and $\Delta x$ for this particular case. For the Inf sq well case, you start with kinetic energy as a function of L. You also have a relationship between L and $\Delta x$ which you can use that to substitute out L and get a relationship between T and $\Delta x$ for this particular case.
Though I won't discuss the integrands of 5-7 here, they are quite important. Feel free to post any questions or comments about them here.
Problem 8 provides an example of a state for which the confinement of the electron changes fairly dramatically as a function of time. I think the KE will also vary in a complementary manner. That is, It will be largest when the wave-function is most confined as oscillate as a function of time, like x^2, but 180 degrees out of phase.
I believe that some people found problem 4 to be a little tricky or confusing. My approach to problem 4 is on the last page. For the HO GS you start with kinetic energy as a function of a. And we also have a relationship between a and $\Delta x$. You can use that to substitute out a and get a relationship between T and $\Delta x$ for this particular case. For the Inf sq well case, you start with kinetic energy as a function of L. You also have a relationship between L and $\Delta x$ which you can use that to substitute out L and get a relationship between T and $\Delta x$ for this particular case.
Though I won't discuss the integrands of 5-7 here, they are quite important. Feel free to post any questions or comments about them here.
Problem 8 provides an example of a state for which the confinement of the electron changes fairly dramatically as a function of time. I think the KE will also vary in a complementary manner. That is, It will be largest when the wave-function is most confined as oscillate as a function of time, like x^2, but 180 degrees out of phase.
Saturday, February 9, 2013
Class Notes, Feb 7:
These note are from our Feb 7 class, which was directed toward deepening out understanding of kinetic energy (momentum squared). Understanding kinetic energy and momentum is the the key to understanding quantum physics, in my point-of-view. In classical physics, momentum and kinetic energy are generally associated with motion. In quantum physics, kinetic energy and momentum are associated with confinement. In quantum physics electrons can, and generally do, have significant momentum and kinetic energy without moving at all.
(note: The order I had in mind for these is indicated by the number in the upper right-hand corner of each page, not by their order below.)
(note: The order I had in mind for these is indicated by the number in the upper right-hand corner of each page, not by their order below.)
Thursday, February 7, 2013
Homework 6: one-electron states of molecules and crystals.
One can write molecular wave-functions as linear combination of atomic wave-functions with different center positions. (In my experience, this is the most common way in which to construct them. See, for example, LCAO.)
For example, suppose your are given a generic attractive potential (in 1D) of $U(x)$ for which the electron ground state wave-function is $\psi_o (x)$, and the energy of an electron in this state is $E_o$. You are given all that:
i) an atom-like potential, $U(x)$ (attractive, negative, single well, symmetric, with its minimum at x=0 ),
ii) an atom-like ground state wave-function, $\psi_o (x)$ (a simple, normalized, exponential function such as $e^{-|x|/a}/a^{1/2}$ or, $e^{-x^2/(2a^2}/(a^{1/2} \pi^{1/4})$),
iii) the ground state energy of this atom-like state in this potential, $E_o$.
The idea is -- with these things as given, solved and known: how would you use them to construct one-electron wave-functions for molecules and crystals?
1. Suppose that and electron experiences the double potential,
$U_m (x) = U(x) + U(x-b)$, where U(x) has a simple minimum at x=0 and U(x-b) has an identical minimum at (x-b)=0.
a) Sketch $U_m (x)$
b) Write an expression for a wave-function that might be a reasonable guess for the ground state of this potential. Do this by combining atom-like wave-functions with different center positions.
c) Sketch your wave-function.
d) How would you normalize it, more or less? (You can assume that the atomic wave-functions are initially normalized.) Is it easy or difficult to normalize the molecular wave-function?
(please comment on this below. Is it hard or easy? why?)
2. For the same potential,
a) How might you make a molecular wave-function that would be a reasonable guess for the first excited state of this potential?
b) Sketch your wave-function.
c) how many nodes does this state have?
3. Now consider 4 identical potentials in a row.
For example,$U_m (x) = U(x) + U(x-b) + U(x-2b) + U(x-3b)$.
a) sketch $U_m (x)$.
b) Make a molecular wave-function that might be a reasonable guess for the ground state of this potential by combining atomic wave-functions with different center positions?
c) Sketch your wave-function.
d) Now many excited states can you make (using just the atomic ground state $\psi_o (x)$)?
e) Make them all (write an expression for each one) and sketch each one in a separate graph next to its wave-function. (hint: You are given the atomic wave-functions. What you need to do is write a plus or minus sign in from of them in an informed manner that, for example, makes the molecular states you are creating orthogonal to each other. You know you are done when you cannot make any more that are orthogonal to the ones you already have.)
f) Discuss their energy order. (Which is lowest energy? next lowest?, highest?, why?)
g) How many nodes does each one have?
4. Let's now consider many (N) such identical potentials, all in a row.
a) What does the ground state of this many-well system look like? How would you construct it?
b) Discuss here in this blog the excited states you can create. What are they like? How would you describe them?
===============================================
Problems 1-4 are very important. I would focus a lot of attention on them, especially 4. Problem 4 is too difficult and nuanced for any one person to do alone. It has many layers that can be gradually peeled back and explored. I think the best way to approach it is to post your thoughts and questions about it here, and then you can make progress on it by working together as a class. You will get beaucoup credit for your contributions here.
================================================
5. I would like to add one more problem which is pretty interesting, but not as deep and nuanced as 4 (so i do not want to take too much attention away from 4 by adding this last problem).
a) Do a contour plot illustrating the nature of the state:
$\psi(x,y,z) = (e^{-(r/a)} + e^{-r_b/a})/\sqrt{2 \pi a^3})$, (typo corrected Feb 15)
where
$r_b = \sqrt{(x-b)^2 + y^2 + z^2}$
(what plane did you choose to do your contour plot in? why?)
For example, suppose your are given a generic attractive potential (in 1D) of $U(x)$ for which the electron ground state wave-function is $\psi_o (x)$, and the energy of an electron in this state is $E_o$. You are given all that:
i) an atom-like potential, $U(x)$ (attractive, negative, single well, symmetric, with its minimum at x=0 ),
ii) an atom-like ground state wave-function, $\psi_o (x)$ (a simple, normalized, exponential function such as $e^{-|x|/a}/a^{1/2}$ or, $e^{-x^2/(2a^2}/(a^{1/2} \pi^{1/4})$),
iii) the ground state energy of this atom-like state in this potential, $E_o$.
The idea is -- with these things as given, solved and known: how would you use them to construct one-electron wave-functions for molecules and crystals?
1. Suppose that and electron experiences the double potential,
$U_m (x) = U(x) + U(x-b)$, where U(x) has a simple minimum at x=0 and U(x-b) has an identical minimum at (x-b)=0.
a) Sketch $U_m (x)$
b) Write an expression for a wave-function that might be a reasonable guess for the ground state of this potential. Do this by combining atom-like wave-functions with different center positions.
c) Sketch your wave-function.
d) How would you normalize it, more or less? (You can assume that the atomic wave-functions are initially normalized.) Is it easy or difficult to normalize the molecular wave-function?
(please comment on this below. Is it hard or easy? why?)
2. For the same potential,
a) How might you make a molecular wave-function that would be a reasonable guess for the first excited state of this potential?
b) Sketch your wave-function.
c) how many nodes does this state have?
3. Now consider 4 identical potentials in a row.
For example,$U_m (x) = U(x) + U(x-b) + U(x-2b) + U(x-3b)$.
a) sketch $U_m (x)$.
b) Make a molecular wave-function that might be a reasonable guess for the ground state of this potential by combining atomic wave-functions with different center positions?
c) Sketch your wave-function.
d) Now many excited states can you make (using just the atomic ground state $\psi_o (x)$)?
e) Make them all (write an expression for each one) and sketch each one in a separate graph next to its wave-function. (hint: You are given the atomic wave-functions. What you need to do is write a plus or minus sign in from of them in an informed manner that, for example, makes the molecular states you are creating orthogonal to each other. You know you are done when you cannot make any more that are orthogonal to the ones you already have.)
f) Discuss their energy order. (Which is lowest energy? next lowest?, highest?, why?)
g) How many nodes does each one have?
4. Let's now consider many (N) such identical potentials, all in a row.
a) What does the ground state of this many-well system look like? How would you construct it?
b) Discuss here in this blog the excited states you can create. What are they like? How would you describe them?
===============================================
Problems 1-4 are very important. I would focus a lot of attention on them, especially 4. Problem 4 is too difficult and nuanced for any one person to do alone. It has many layers that can be gradually peeled back and explored. I think the best way to approach it is to post your thoughts and questions about it here, and then you can make progress on it by working together as a class. You will get beaucoup credit for your contributions here.
================================================
5. I would like to add one more problem which is pretty interesting, but not as deep and nuanced as 4 (so i do not want to take too much attention away from 4 by adding this last problem).
a) Do a contour plot illustrating the nature of the state:
$\psi(x,y,z) = (e^{-(r/a)} + e^{-r_b/a})/\sqrt{2 \pi a^3})$, (typo corrected Feb 15)
where
$r_b = \sqrt{(x-b)^2 + y^2 + z^2}$
(what plane did you choose to do your contour plot in? why?)
Wednesday, February 6, 2013
Momentum, kinetic energy, and confinement
This is the third in a sequence of 3 videos I made about kinetic energy and its relationship to confinement, etc. It is posted first because originally the other two are delayed due to upload problems. Actually, it might be fine to start with this one. The first two are pretty focused on calculating expectation values, whereas this one is more focused on considering and discussing the nature of momentum, KE and confinement and how they may be related. In it we examine the nature of a electron state (mixed state) in which the degree of confinement varies with time. The comment section below would be a great place for any questions or thoughts you have about this important subject. Sometimes I am not sure if many people actually view these videos, and whether or not I should continue to make more. So if you do I would appreciate knowing that. Just even a short comment or a vote in the poll would be appreciated.
PS. Here is the 1st video from the sequence I made on Tuesday.
The 2nd video from the sequence about momentum, KE and confinement (part2) is embedded below. I recommend watching the 1st 10 minutes or so of this video, and then perhaps skipping ahead to part 3. After about the 10 minute mark this one gets into a pretty tedious calculation. Part 3, on the other hand, (which is up above in this post) focuses more on relationships and meaning and less on detailed calculation. Part 3 may be more interesting.
PS. Here is the 1st video from the sequence I made on Tuesday.
The 2nd video from the sequence about momentum, KE and confinement (part2) is embedded below. I recommend watching the 1st 10 minutes or so of this video, and then perhaps skipping ahead to part 3. After about the 10 minute mark this one gets into a pretty tedious calculation. Part 3, on the other hand, (which is up above in this post) focuses more on relationships and meaning and less on detailed calculation. Part 3 may be more interesting.
Monday, February 4, 2013
Homework 4 solutions: how the hydrogen atom gets its size.
The enclosed are some solutions for HW 4. I melded problems 6 and 8 together in the solutions, although you were not required to do that. That problem shows how the electron's (ground state) wave-function in a hydrogen atom "decided" that 0.053 nm was just the right size. Sort of like Goldilocks, it "realized" that if its size were larger then it would not have a large enough potential energy, while if it were smaller (more confined to the region around the proton), then its kinetic energy would be too high. So that is how the hydrogen atom got its size.
It is the last part that is uniquely quantum, and an example of how the nature of quantum KE, which is unusual, influences many basic phenomena.
One side note on problem 9: I don't know if anyone did that problem. I had meant to make the state fr that problem and equal mix of $Psi_o$ and $Psi_2$, which I am pretty sure has a lot of time dependence for T and U because that mixed state "expands" and "contracts" quite a bit as a function of time. Calculating x^2 for that mixed state is now on HW 5 as an advanced problem; it is pretty interesting I think.
Please feel free to post comments and questions and initiate discussion here. Hope fully these are interesting and stimulating topics.
It is the last part that is uniquely quantum, and an example of how the nature of quantum KE, which is unusual, influences many basic phenomena.
One side note on problem 9: I don't know if anyone did that problem. I had meant to make the state fr that problem and equal mix of $Psi_o$ and $Psi_2$, which I am pretty sure has a lot of time dependence for T and U because that mixed state "expands" and "contracts" quite a bit as a function of time. Calculating x^2 for that mixed state is now on HW 5 as an advanced problem; it is pretty interesting I think.
Please feel free to post comments and questions and initiate discussion here. Hope fully these are interesting and stimulating topics.
Sunday, February 3, 2013
Small research project using mathematica.
I have a small research project for someone who can program a bit in Mathematica. The ability to create something that will create graphs of simple functions and display them in a flip-book type format (time animation) that will run with Mathematica7.0.1 (on a Mac Book Pro running 10.6.8) would be the ideal. Please email me at zacksc@gmail.com if interested. Thanks.
Saturday, February 2, 2013
Homework 5: momentum, confinement and kinetic energy.
due Friday, Feb 8.
(corrections: problems 3 & 7, Tuesday evening (see comments))
(edited: Sunday Feb 3, intro and problem 8)
(Please report any typos you find and ask about anything that is unclear, strange, etc.)
This is probably our most important homework so far in this class. I think it will be pivotal in helping develop your understanding of key aspects of quantum physics which will allow us to make the transition from describing atoms and other single-well systems to the description of molecules, semiconductors and other quantum materials. Feel free to ask questions and discuss the problems. These are hard problems and I think it is helpful to work with actual groups and people, and to engage in questions and discussion here.
Problems 1-4 are related to confinement, momentum and kinetic energy. As you know, the Heisenberg relation is often expressed as the inequality $\Delta x \Delta p \ge \hbar / 2$. In the first 4 problems we will do some calculations of $\Delta x$ and $\Delta p$ (and some closely related quantities) for specific systems and states. This will provide a chance to examine the Heisenberg inequality from a physics point-of-view, which is somewhat different from perspectives that are pervasive in popular culture (which tend to fixate on the word "uncertainty"). Uncertainty is a complex word with many possible meanings. Inequalities, such as the one above, refer to the precision with which one can localize a wave-packet, and the need for short wave-lengths in doing so. Such relationships are present in many wave theories, string, E&M, water ..., in which one can envision deconstructing a localized packet into components of precise (well-defined) wavelength.
Problems 5-7 all focus on kinetic energy integrands, especially distinguishing regions of space that contribute negatively to the kinetic energy from the regions which contribute positively to KE. This is a novel and important aspect of quantum mechanics. Another perhaps novel thing is that all the kinetic energies in 5-7 are independent of time. However, this is not generally the case for KE in quantum physics.
Problem 8 provides a relatively simple example of a state (wave-function) in which KE and PE of an electron vary (in a complementary way) as a function of time. I think if you take the time to do 8, it provides a perspective that allows the whole thing to make more sense. Feel free to start with part b), which is mathematically a little easier than a).
1. a) Calculate $\Delta x$ and $\Delta p$ for an electron in the ground state of a harmonic oscillator.
b) What is the product $\Delta x \Delta p$ for an electron in this state? Does it depend on time?
2. a) Calculate $\Delta x$ and $\Delta p$ for an electron in the ground state of an infinite square well (of width L).
b) What is the product $\Delta x \Delta p$ for an electron in this state?
3. Show that the Heisenberg relation can be recast as a relationship between kinetic energy and confinement, namely,
$\bar{T} \geq \hbar^2/(4 m (\Delta x)^2$, aaarrrrg, this is incorrect.
$\bar{T} \geq \hbar^2/(8 m (\Delta x)^2$, <---- this one is corrrect i think.
where $\bar{T}$ is an expectation value of kinetic energy and $\Delta x = \sqrt{\bar{x^2}-\bar{x}^2}$ is a length scale which provides a measure of the degree of confinement of an electron.
4. Write $\bar{T}$ in terms of $(\Delta x)^2$, m and $\hbar$ for:
a) an electron in the ground state of a harmonic oscillator.
b) an electron in the ground state of an infinite square well.
(these are different, right?)
5. a) Graph the integrand from the integral that arises in the calculation of $\bar{T}$ for an electron in the ground state of a harmonic oscillator.
b) Although $\bar{T}$ is positive, there are regions of x that contribute negatively to the integral (regions that diminish $\bar{T}$). Where are there? (That is, over what range(s) of x is the integrand negative?)
c) Indicate those regions in your graph. Do you notice anything about the nature of the curvature of $\psi (x)$ for those regions?
6. a) Graph the integrand from the integral that arises in the calculation of $\bar{T}$ for an electron in the ground state of a finite square well. (Note: For this problem you are not expected to calculate T or to know the exact state for this problem. Please use the form of the ground state that was provided in problem 7 of HW 4. I think you can do this entire problem using that form (and without evaluating A or B).)
b) Although $\bar{T}$ is positive, there are regions of x that contribute negatively to the integral (regions that diminish $\bar{T}$). Where are there? (That is, over what range(s) of x is the integrand negative?)
c) Indicate those regions in your graph. Do you notice anything about the nature of the curvature of $\psi (x)$ for those regions?
7. In this problem we would like to sketch the integrand associated with the $\bar{T}$ calculation for a double square-well focusing in particular on the nature of the contribution to $\bar{T}$ that arises from the region between the two wells. A double square-well refers to two finite square wells. In this case, let's put the origin of coordinates between the wells, define a center-to-center distance of b, and the width of the wells as L. In equations:
$U(x) = -V$, for (-b/2) - (L/2) $\leq x \leq$ (-b/2) + (L/2),
$U(x) = -V$, for (b/2) - (L/2) $\leq x \leq$ (b/2) + (L/2),
$U(x) = 0$, elsewhere.
(In this case, the two wells are identical in depth (measured in energy) and width (L). We assume that b is greater than L, so that the wells are not overlapping and that b is not too large, so that the two wells are close to each other. (We will learn how to define what "close" means. That is an important question! (thanks for asking).
Additionally let's use the following notation for the ground state:
$\psi(x) = A cos(k(x-b/2))$, for (b/2) - (L/2) $\leq x \leq$ (b/2) + (L/2),
$\psi(x) = B e^{-\gamma (x-(b+L)/2)}$, for $x \geq (b+L)/2)$,
$\psi(x) = C cosh(\gamma x)$, for (-b/2) + (L/2) $\leq x \leq$ (b/2) - (L/2),
Where the A cos( ) term is for the wave-function within the region of the right-hand-well, which is centered at b/2, I believe; the $B e^{-( )}$ term is for the region beyond the right-hand-well, and the very important C cosh( ) term is for the region between the two wells
a) graph the potential U(x) as a function of x (for b = 2L approximately).
b) graph the ground state wave-function $\psi (x)$ as a function of x. (I would suggest using an assumed $\gamma$ of roughly 3/b.)
c) calculate and then graph the second derivative of the wave function for these regions (leaving A, B and C undetermined)
d) graph the integrand of the kinetic energy calculation for this double-well system,
$\psi (x) (-d^2 \psi (x) / dx^2)$ for these regions.
e) What is the sign of the contribution to $\bar{T}$ from the region between the wells? Why might this be relevant to understanding molecular bonding? Thinking about K.E. and confinement, what does it signify?
8. Advanced. (I would recommend reading the whole problem and then starting with the calculation of part b. I think that is a lot less difficult than calculating $\bar{T}$ for this mixed state.) All of the kinetic energy expectation values we have calculated so far have been "constants of motion", that is, not dependent on time. This is a different from what you may be used to, since in a classical harmonic oscillator, or a wave on a string, etc., we expect the kinetic and potential energies to oscillate with time. This can happen in QM also, however, just not for the pure states (energy eigenstates) that we have been studying.
a) Show that for an electron in a harmonic oscillator in the mixed state that is an equal mix of the ground state and 2nd excited state, the kinetic and potential energy each oscillate as a function of time. What is the period of the oscillation? How does it relate to an oscillation in the size of the wave-function?
e.g., at t=0, $\psi(x) = (\psi_o (x) - \psi_2 (x))/\sqrt{2}$
Start here ==> b) Calculate $\bar{x^2}$ as a function of time for an electron in this mixed state. What is its smallest value? What is is largest value? Graph it (vs t). How is $\bar{U}$ related to $\bar{x^2}$? How would you guess that $\bar{T}$ might be related to $\bar{U}$? (Feel free to discuss here. Is there a simple relationship between $\bar{T}$ and $\bar{U}$? This is not obvious so anything you say or ask will be good.)
(corrections: problems 3 & 7, Tuesday evening (see comments))
(edited: Sunday Feb 3, intro and problem 8)
(Please report any typos you find and ask about anything that is unclear, strange, etc.)
This is probably our most important homework so far in this class. I think it will be pivotal in helping develop your understanding of key aspects of quantum physics which will allow us to make the transition from describing atoms and other single-well systems to the description of molecules, semiconductors and other quantum materials. Feel free to ask questions and discuss the problems. These are hard problems and I think it is helpful to work with actual groups and people, and to engage in questions and discussion here.
Problems 1-4 are related to confinement, momentum and kinetic energy. As you know, the Heisenberg relation is often expressed as the inequality $\Delta x \Delta p \ge \hbar / 2$. In the first 4 problems we will do some calculations of $\Delta x$ and $\Delta p$ (and some closely related quantities) for specific systems and states. This will provide a chance to examine the Heisenberg inequality from a physics point-of-view, which is somewhat different from perspectives that are pervasive in popular culture (which tend to fixate on the word "uncertainty"). Uncertainty is a complex word with many possible meanings. Inequalities, such as the one above, refer to the precision with which one can localize a wave-packet, and the need for short wave-lengths in doing so. Such relationships are present in many wave theories, string, E&M, water ..., in which one can envision deconstructing a localized packet into components of precise (well-defined) wavelength.
Problems 5-7 all focus on kinetic energy integrands, especially distinguishing regions of space that contribute negatively to the kinetic energy from the regions which contribute positively to KE. This is a novel and important aspect of quantum mechanics. Another perhaps novel thing is that all the kinetic energies in 5-7 are independent of time. However, this is not generally the case for KE in quantum physics.
Problem 8 provides a relatively simple example of a state (wave-function) in which KE and PE of an electron vary (in a complementary way) as a function of time. I think if you take the time to do 8, it provides a perspective that allows the whole thing to make more sense. Feel free to start with part b), which is mathematically a little easier than a).
1. a) Calculate $\Delta x$ and $\Delta p$ for an electron in the ground state of a harmonic oscillator.
b) What is the product $\Delta x \Delta p$ for an electron in this state? Does it depend on time?
2. a) Calculate $\Delta x$ and $\Delta p$ for an electron in the ground state of an infinite square well (of width L).
b) What is the product $\Delta x \Delta p$ for an electron in this state?
3. Show that the Heisenberg relation can be recast as a relationship between kinetic energy and confinement, namely,
$\bar{T} \geq \hbar^2/(4 m (\Delta x)^2$, aaarrrrg, this is incorrect.
$\bar{T} \geq \hbar^2/(8 m (\Delta x)^2$, <---- this one is corrrect i think.
where $\bar{T}$ is an expectation value of kinetic energy and $\Delta x = \sqrt{\bar{x^2}-\bar{x}^2}$ is a length scale which provides a measure of the degree of confinement of an electron.
4. Write $\bar{T}$ in terms of $(\Delta x)^2$, m and $\hbar$ for:
a) an electron in the ground state of a harmonic oscillator.
b) an electron in the ground state of an infinite square well.
(these are different, right?)
5. a) Graph the integrand from the integral that arises in the calculation of $\bar{T}$ for an electron in the ground state of a harmonic oscillator.
b) Although $\bar{T}$ is positive, there are regions of x that contribute negatively to the integral (regions that diminish $\bar{T}$). Where are there? (That is, over what range(s) of x is the integrand negative?)
c) Indicate those regions in your graph. Do you notice anything about the nature of the curvature of $\psi (x)$ for those regions?
6. a) Graph the integrand from the integral that arises in the calculation of $\bar{T}$ for an electron in the ground state of a finite square well. (Note: For this problem you are not expected to calculate T or to know the exact state for this problem. Please use the form of the ground state that was provided in problem 7 of HW 4. I think you can do this entire problem using that form (and without evaluating A or B).)
b) Although $\bar{T}$ is positive, there are regions of x that contribute negatively to the integral (regions that diminish $\bar{T}$). Where are there? (That is, over what range(s) of x is the integrand negative?)
c) Indicate those regions in your graph. Do you notice anything about the nature of the curvature of $\psi (x)$ for those regions?
7. In this problem we would like to sketch the integrand associated with the $\bar{T}$ calculation for a double square-well focusing in particular on the nature of the contribution to $\bar{T}$ that arises from the region between the two wells. A double square-well refers to two finite square wells. In this case, let's put the origin of coordinates between the wells, define a center-to-center distance of b, and the width of the wells as L. In equations:
$U(x) = -V$, for (-b/2) - (L/2) $\leq x \leq$ (-b/2) + (L/2),
$U(x) = -V$, for (b/2) - (L/2) $\leq x \leq$ (b/2) + (L/2),
$U(x) = 0$, elsewhere.
(In this case, the two wells are identical in depth (measured in energy) and width (L). We assume that b is greater than L, so that the wells are not overlapping and that b is not too large, so that the two wells are close to each other. (We will learn how to define what "close" means. That is an important question! (thanks for asking).
Additionally let's use the following notation for the ground state:
$\psi(x) = A cos(k(x-b/2))$, for (b/2) - (L/2) $\leq x \leq$ (b/2) + (L/2),
$\psi(x) = B e^{-\gamma (x-(b+L)/2)}$, for $x \geq (b+L)/2)$,
$\psi(x) = C cosh(\gamma x)$, for (-b/2) + (L/2) $\leq x \leq$ (b/2) - (L/2),
Where the A cos( ) term is for the wave-function within the region of the right-hand-well, which is centered at b/2, I believe; the $B e^{-( )}$ term is for the region beyond the right-hand-well, and the very important C cosh( ) term is for the region between the two wells
a) graph the potential U(x) as a function of x (for b = 2L approximately).
b) graph the ground state wave-function $\psi (x)$ as a function of x. (I would suggest using an assumed $\gamma$ of roughly 3/b.)
c) calculate and then graph the second derivative of the wave function for these regions (leaving A, B and C undetermined)
d) graph the integrand of the kinetic energy calculation for this double-well system,
$\psi (x) (-d^2 \psi (x) / dx^2)$ for these regions.
e) What is the sign of the contribution to $\bar{T}$ from the region between the wells? Why might this be relevant to understanding molecular bonding? Thinking about K.E. and confinement, what does it signify?
8. Advanced. (I would recommend reading the whole problem and then starting with the calculation of part b. I think that is a lot less difficult than calculating $\bar{T}$ for this mixed state.) All of the kinetic energy expectation values we have calculated so far have been "constants of motion", that is, not dependent on time. This is a different from what you may be used to, since in a classical harmonic oscillator, or a wave on a string, etc., we expect the kinetic and potential energies to oscillate with time. This can happen in QM also, however, just not for the pure states (energy eigenstates) that we have been studying.
a) Show that for an electron in a harmonic oscillator in the mixed state that is an equal mix of the ground state and 2nd excited state, the kinetic and potential energy each oscillate as a function of time. What is the period of the oscillation? How does it relate to an oscillation in the size of the wave-function?
e.g., at t=0, $\psi(x) = (\psi_o (x) - \psi_2 (x))/\sqrt{2}$
Start here ==> b) Calculate $\bar{x^2}$ as a function of time for an electron in this mixed state. What is its smallest value? What is is largest value? Graph it (vs t). How is $\bar{U}$ related to $\bar{x^2}$? How would you guess that $\bar{T}$ might be related to $\bar{U}$? (Feel free to discuss here. Is there a simple relationship between $\bar{T}$ and $\bar{U}$? This is not obvious so anything you say or ask will be good.)
Subscribe to:
Comments (Atom)