Homework 7: electrons in metals

This homework gives you a chance to explore electrons in metals, current flow and things like that. It will stay at a pretty high-level: we start with an expression for energy vs k, which we have discussed and tried to justify to some degree. We also take as "given", a straight-forward, easy to use relationship for velocity. Our metal is one-dimensional (1D) with a particular electron density, $10^8$ electrons/cm and a particular filling of the band (1/2 filled).

$E_k = E_o -(B/2) cos (bk)$, where B is in eV and typically around 1 to 8 eV.

$v_k = (1/\hbar) \partial{E_k}/\partial{k}$

1. Consider a metal with one well per 0.1 nm ($b = 0.1 nm$) and one (itinerant=non-local) electron per well. That leads to an electron density of 1 electron per 0.1 nm, or, equivalently, $10^8$ electrons/cm, right? With one electron per well we will get, i think, a half-filled band, that is, all the states between $k = -\pi/2b$ and $k = \pi/2b$ are filled. Assume that B = 4 eV.
a) Sketch $E_k$ vs k and indicate on your sketch where the boundary between filled and empty states is.
b) What is the speed of an electron in a boundary state, i.e., the state $\psi_k$ with $k = \pi/2b$ (also known as $k_f$). What is it in cm/sec?  (feel free to post here for a quick check and comparison with others)
c) When there are an equal number of electrons in k and -k states, the net current is zero. However, an electric field can skew the occupation boundaries so that that balance is disrupted. Suppose that the balance is skewed so that 1 in 1000 right-moving electrons are uncompensated. What is the net current carried by these electrons. [Hint: You can assume all of them have essentially the same speed and use the equation I=nev to calculate the current in electrons per second or in coulombs per second. Here n is the density of current carrying, uncompensated electrons (in electrons per cm), e is the charge of an electron, and v is the speed (from b). Do you get a current more or less in the micro-ampere range. What is it?

2. Compare the speed of the electron in problem 7 of the midterm, to the speed of an electron in the "band state" $\psi_k$, with $k=\pi/2b$ with B = 1 eV. Are they similar at all? Feel free to comment/discuss here. (Your first line could be: "how do we define the speed of the electron in problem 7?")

3. What is the nature of the time dependence of the crystal state:
$\psi_{o,k} (x,t) = \sum^\infty_{n= -\infty} e^{inkb} \psi_o (x-nb)$.
 Is this an eigenstate or a mixed state?
Please ask questions about this, comment or share your thoughts below...

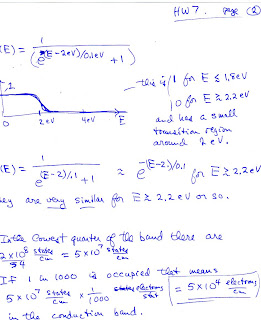
4. Graph the function $f(E) = 1/(e^{(E-2)/.1} + 1)$ from about zero to 5. Describe it.

5. Compare the functions $f(E) = 1/(e^{(E-2)/.1} + 1)$ and $f(E) = e^{-(E-2)/.1}$. Where are most different? Are they similar over any region? Why?

6. A conduction band of a semi-conductor can be just like that of a metal in terms of the nature of the states $\psi_k$ and the E vs k relation, but it is completely different in terms of the occupation of the states. Typically in a semi-conductor only some states near the bottom of the conduction band are occupied at all.
a) Suppose 1 in 1000 of the states in the lowest quarter of the band (between $k = -\pi/4b$ and $\pi/4b$) are occupied and the rest of the conduction band is empty. How many electrons/cm is that in the conduction band? (units are electrons/cm)


Appendix:
This energy vs k relation (called a "dispersion relation"),
$E_k = E_o -(B/2) cos (bk)$,
refers to the energies of states of the form:

$\psi_{o,k} (x) = \sum^\infty_{n= -\infty} e^{inkb} \psi_o (x-nb))$.
These are the states made of "combinations of atomic orbitals", as we discussed and sketched last week.

Although it is not at all obvious, once you put in their time dependence (see problem 4), these states have a velocity given by the equation:
$v_k = (1/\hbar) \partial{E_k}/\partial{k}$
(which you might notice is proportional to k at low kb just like for free electron states.)

Oh, by the way, a note on terminology:
1) the "height" of the band, which is B since the band goes from a lowest energy of $E_o - B/2$ to a maximum energy of $E_o + B/2$ (at $k=\pi/b$, is generally called "bandwidth".

What looks like it should be called width, the interval from $-\pi/b$ to $\pi/b$, is called the Brillouin zone (or sometimes 1st Brillouin zone). The points $-\pi/b$ to $\pi/b$ are called the "Brillouin zone edge."

Solution notes: