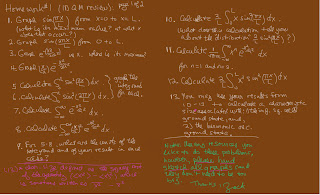One of our fellow students sent me an email of a blog with a nice the derivation of the Laplacian.
http://skisickness.com/2009/11/20/
Thursday, January 31, 2013
Midterm, Feb 19: midterm preparation; Quiz.
Our midterm will be on February 19. I'll post more regarding what to study and emphasize, and how I would suggest you prepare for that, etc. The following is a rough guide and a start to that conversation. Basically, our primary point-of-reference and guide is the homework problems, but we can flesh that out a little.
I think it is a good idea to be familiar with almost all of the energy eigenstate wave-functions we have discussed. These include:
the first 3 states of the 1D harmonic oscillator,
the first 3 states of the 1D infinite square well placed between x=0 and x=L,
the first 3 states of the 1D infinite square well placed between x=-L/2 and x=L/2 (we haven't actually looked at this one yet, but I think you should know these states as well),
the ground state of hydrogen,
the 4 excited states of hydrogen in the r, x, y, z notation.
For good measure I would add:
the states associated with the first 3 energy levels of the 2D harmonic oscillator, and,
the states associated with the first 2 energy levels of the 3D harmonic oscillator (1 ground state + 3 1st-excited states).
Quantum mechanics is pursuit that takes you into the world of eigenfunctions. If you don't learn to hear and understand their language, you will be lost. Time spent with eigenfunctions (wave-functions) is time well spent. If you can forget them, then your relationship is not sufficiently intimate. It goes without saying that you would wish to know the energies of each of the above states and how to use that to add in their time dependence. (All quantum states are time dependent.)
Additionally, you would like to know how to calculate expectation values for an electron in one of these states, or in some simple combinations of them. One would also wish to have a reasonable understanding of what expectation values are trying to communicate. And also, to understand how and why expectation values for mixed states tend to be time dependent, while those calculated for energy eigenstates are not.
To help you assess your depth of understanding and your ability to communicate that in a test-type format, I think we should have a quiz soon. I am thinking of a closed book, one or one-a-half hour quiz. You may use one page of notes. (Your page of notes should have only basic stuff, eigenfunctions, energies, operator definitions, etc., not because you don't know them by heart, but just to reassure you when you are working in a stressful situation. Also a bunch of definite integrals*, but no solved problems please.) I think that taking this quiz in a simulated test environment in your own home may help you gauge your readiness for the midterm. Please let me know when you think you can be ready.
I think it is a good idea to be familiar with almost all of the energy eigenstate wave-functions we have discussed. These include:
the first 3 states of the 1D harmonic oscillator,
the first 3 states of the 1D infinite square well placed between x=0 and x=L,
the first 3 states of the 1D infinite square well placed between x=-L/2 and x=L/2 (we haven't actually looked at this one yet, but I think you should know these states as well),
the ground state of hydrogen,
the 4 excited states of hydrogen in the r, x, y, z notation.
For good measure I would add:
the states associated with the first 3 energy levels of the 2D harmonic oscillator, and,
the states associated with the first 2 energy levels of the 3D harmonic oscillator (1 ground state + 3 1st-excited states).
Quantum mechanics is pursuit that takes you into the world of eigenfunctions. If you don't learn to hear and understand their language, you will be lost. Time spent with eigenfunctions (wave-functions) is time well spent. If you can forget them, then your relationship is not sufficiently intimate. It goes without saying that you would wish to know the energies of each of the above states and how to use that to add in their time dependence. (All quantum states are time dependent.)
Additionally, you would like to know how to calculate expectation values for an electron in one of these states, or in some simple combinations of them. One would also wish to have a reasonable understanding of what expectation values are trying to communicate. And also, to understand how and why expectation values for mixed states tend to be time dependent, while those calculated for energy eigenstates are not.
To help you assess your depth of understanding and your ability to communicate that in a test-type format, I think we should have a quiz soon. I am thinking of a closed book, one or one-a-half hour quiz. You may use one page of notes. (Your page of notes should have only basic stuff, eigenfunctions, energies, operator definitions, etc., not because you don't know them by heart, but just to reassure you when you are working in a stressful situation. Also a bunch of definite integrals*, but no solved problems please.) I think that taking this quiz in a simulated test environment in your own home may help you gauge your readiness for the midterm. Please let me know when you think you can be ready.
Wednesday, January 30, 2013
Guide to Homework 4, updated.
This was updated Friday (Feb 1) with some extra graphs at the end related to problem 10, which is an important problem and not really so difficult. (Much less difficult than 9, for example.)
These are notes related to preparing for, understanding and doing HW 4:
For the quantum systems we have studied so far: the infinite square well, the harmonic oscillator, and the -1/r potential ("H-atom"), it is possible to find exact solutions to the differential equation that the wave equation (Schrodinger) equation provides. Specifically we have look in some detail at the first 3 states of the infinite square well and 1DHO and 2DHO, and at the ground state and 1st excited states of the -1/r potential using the {x, y, z, r} choice for the 4 excited states for the latter system (H-atom).
In a lot of quantum systems one would like to study and understand, one can't solve the differential equation in a normal way. One of the methods that is very widely used is to guess a solution. The art of this method lies in making educated guesses for wave-functions. This approach of making educated guesses is call the "variational method", because in some of the guessed wave-functions there is a parameter that can be varied (like "a" for the wave-functions in problems 4, 5 and 6.) Generally what one does with a guessed or variational wave function is to calculate the energy of that wave-function. One can do this by calculating the expectation value of the kinetic and potential energies and adding them together. That is what you are asked to do in problems 4-6.
Problems 3 is not of this type (and neither is 7). In problem 3 you are asked to calculate the expectation value of the kinetic energy, T, and the potential energy, U, using the exact solution for the ground state of the infinite square well, which you know already.
Problem 7 is also not a variational method problem. In 7 you are asked to find the ground state of a finite square well using a fairly standard boundary matching approach (where you require continuity and smoothness at the boundary). The forms of the solution in the two regions in this problem are not guesses, but rather come from solutions to the time independent Schrodinger equation. It is from the Schrodinger equation, which is different inside and outside the well because inside U(x)= -V and outside U(x)= 0, that one gets a relationship between $\gamma$ and k. So the method in problem 7 is quite different from that in 4-6. The most important part of 7 are the questions in c) and d) (is this value of k larger or smaller…?, why?), though you have to do the whole thing to get to that.
Regarding the method in 7, I think you have some experience in boundary condition matching from 101a. The key thing for that method is that E is the same inside and outside the well. that is what makes the endeavor of matching conclusive; otherwise there would be one too many parameters. The graph in part c) represents a visual way of finding a solution. Where the two curves intersect is a value of k that satisfies both the differential equations and the boundary conditions. I think one can tell from that if the value of k is larger or smaller than that for the infinite square well (which is pi/L, right?)
Problems 1 and 2 are introducing a form of wave-function that will be used for guessed molecular states, probably next week. The wave-function of problem 2 is also related to what one typically uses for electron states in semiconductors (and other crystalline solids). (Imagine repeating this over an over with different "rb" values and getting a wave-function with lots and lots of peaks (each one centered over a different atom). (Note however that this is a one-electron wave-function. We will need lots of states like this (an entire band of them) and then consider a description of electrons in semiconductors analogous to the approach to the periodic table: namely filling one-electron states one after another.)
Here I set b=2 and a =1, since otherwise WA might treat b as a 2nd variable...
Check these graphs out also. They illustrate the nature of the integrand for problem 10, in which you were asked to graph the integrand associated with the T calculation for an electron in the ground state wave-function if the 1DHO.
These are notes related to preparing for, understanding and doing HW 4:
For the quantum systems we have studied so far: the infinite square well, the harmonic oscillator, and the -1/r potential ("H-atom"), it is possible to find exact solutions to the differential equation that the wave equation (Schrodinger) equation provides. Specifically we have look in some detail at the first 3 states of the infinite square well and 1DHO and 2DHO, and at the ground state and 1st excited states of the -1/r potential using the {x, y, z, r} choice for the 4 excited states for the latter system (H-atom).
In a lot of quantum systems one would like to study and understand, one can't solve the differential equation in a normal way. One of the methods that is very widely used is to guess a solution. The art of this method lies in making educated guesses for wave-functions. This approach of making educated guesses is call the "variational method", because in some of the guessed wave-functions there is a parameter that can be varied (like "a" for the wave-functions in problems 4, 5 and 6.) Generally what one does with a guessed or variational wave function is to calculate the energy of that wave-function. One can do this by calculating the expectation value of the kinetic and potential energies and adding them together. That is what you are asked to do in problems 4-6.
Problems 3 is not of this type (and neither is 7). In problem 3 you are asked to calculate the expectation value of the kinetic energy, T, and the potential energy, U, using the exact solution for the ground state of the infinite square well, which you know already.
Problem 7 is also not a variational method problem. In 7 you are asked to find the ground state of a finite square well using a fairly standard boundary matching approach (where you require continuity and smoothness at the boundary). The forms of the solution in the two regions in this problem are not guesses, but rather come from solutions to the time independent Schrodinger equation. It is from the Schrodinger equation, which is different inside and outside the well because inside U(x)= -V and outside U(x)= 0, that one gets a relationship between $\gamma$ and k. So the method in problem 7 is quite different from that in 4-6. The most important part of 7 are the questions in c) and d) (is this value of k larger or smaller…?, why?), though you have to do the whole thing to get to that.
Regarding the method in 7, I think you have some experience in boundary condition matching from 101a. The key thing for that method is that E is the same inside and outside the well. that is what makes the endeavor of matching conclusive; otherwise there would be one too many parameters. The graph in part c) represents a visual way of finding a solution. Where the two curves intersect is a value of k that satisfies both the differential equations and the boundary conditions. I think one can tell from that if the value of k is larger or smaller than that for the infinite square well (which is pi/L, right?)
Problems 1 and 2 are introducing a form of wave-function that will be used for guessed molecular states, probably next week. The wave-function of problem 2 is also related to what one typically uses for electron states in semiconductors (and other crystalline solids). (Imagine repeating this over an over with different "rb" values and getting a wave-function with lots and lots of peaks (each one centered over a different atom). (Note however that this is a one-electron wave-function. We will need lots of states like this (an entire band of them) and then consider a description of electrons in semiconductors analogous to the approach to the periodic table: namely filling one-electron states one after another.)
Here I set b=2 and a =1, since otherwise WA might treat b as a 2nd variable...
Check these graphs out also. They illustrate the nature of the integrand for problem 10, in which you were asked to graph the integrand associated with the T calculation for an electron in the ground state wave-function if the 1DHO.
Saturday, January 26, 2013
Homework 4: kinetic energy.
(due Friday by 3 PM)
Wednesday, 2 pm: (i just added an extra-credit problem (10) which will be relevant to understanding molecules and crystals.)
Up to this point, we have focused a lot of our attention on wave-functions and degeneracy, and applied that to understanding the some of the periodic table and the geometry of bonding for a few elements (using the 1st-excited states of a -1/r potential).
At this point we can deepen our understanding of quantum physics by turning our attention to energy. Kinetic energy, particularly when associated with confinement, plays a huge role in the quantum world. The interplay and competition between kinetic and potential energy is very important to the phenomena of quantum physics. It can help us understand the size of quantum systems, including the hydrogen atom, the length of chemical bonds and why some materials are insulators instead of metals, as well as some other things. This assignment helps us begin that endeavor.
1. Referring to the enclosed (scanned) notes for clarification as needed,
a) graph exp[-rb/a] as a function of x along the x axis, where rb=sqrt[(x-b)^2+y^2+z^2]
b) do a contour plot to illustrate the nature of exp[-rb/a]
2.
a) graph exp[-r/a] + exp[-rb/a] as a function of x along the x axis.
b) do a contour plot to illustrate the nature of (exp[-r/a] + exp[-rb/a]).
3.
a) Calculate the expectation value of the kinetic energy (T) for the ground state of a 1D infinite square well.
b) Calculate the expectation value of the potential energy (U) for the ground state of a 1D infinite square well.
4. Note that one can calculate T without reference to any particular potential function. In the world of 1D quantum, consider an electron (of mass m) in a state in the form of a 1D normalized gaussian, i.e., $\psi (x) = (a \sqrt \pi)^{-1/2} e^{-x^2/2a^2}$:
a) calculate T (the expectation value of the kinetic energy) and,
b) graph the expectation value of T as a function of a.
5. On the other hand, potential energy (U) expectation values require both a potential, U(x) and a wave-function, $\psi(x)$.
a) Considering a as a parameter able to take on any positive, real value, calculate the expectation value of U for an electron in a state of the form $\psi (x) = (a \sqrt \pi)^{-1/2} e^{-x^2/2a^2}$, in a potential $U(x) = (1/2)kx^2$.
b) graph the expectation value of U as a function of a.
c) find the minimum of T + U (expectation values). At what value of a does that occur? What are the values of T and U at that minimum?
6. For a state that looks like the hydrogen atom electron ground state, but with a allowed to take any value (as in 4 and 5), one can show that T=$\hbar^2/(2ma^2)$ and that
U=$-e^2/a$ (see problem 8 for how one gets this). You can include a $1/(4 \pi \epsilon_o)$ if you prefer that unit system).
a) Show that $\hbar^2/(2ma^2)$ has units of energy,
b) Find the value of a that minimizes E=T + U and the value of T, U and E at that value of a.
c) Are E, T and U positive or negative? Why? (for each one)
7. Consider a 1D finite square well for which the potential is zero everywhere outside the well and -V inside the well. (V, the depth of our attractive well, is a positive number with units of energy.) Assume a width of L, and put the center of the well at x=0.
a) Assuming the ground state is of the form $A cos(kx)$ in the well (A and k undetermined) and $B e^{-\gamma (x-L/2)}$ outside the well, show that you can get a relation between k and $\gamma$ of the form -k*tan(kL/2) =$-\gamma$.
b) Additionally, gamma and k are related since $\hbar^2 k^2/2m = E + V$ and
$\hbar^2 \gamma^2 / (2m) = -E$ (where V is positive and E, the global separation parameter called the energy, is less than zero).
Write $\gamma$ as a function of V and k.
Why is E negative?
c) Anyway you can assume gamma is pretty much constant for small k (why?), and then graph the tan function and 1/k on the same graph to get the actual value of k for the ground state (graphically and approximately). Here is the question:
Is this value of k larger or smaller than the one you would get for an infinite square well of the same width?
d) and even more important: How do you explain that???
8. Extra credit. Calculate the expectation value of T for a hydrogen atom ground state wave function. (take 2 derivatives, integrate...). Do the same for U (i.e., integrate -1/r ...). (This is not actually that difficult as i thought at first since it is only radial derivatives and integrals, i think.)
9. Extra credit/Advanced problem. Consider an electron in a 1DHO in the mixed state sqrt(1/2)(Psi0(x,t) + Psi1(x,t)). Calculate and graph U and T (expectation values) as a function of t.
10. extra credit. For an electron in the ground state of a 1DHO, the calculation of T (the expectation value of the kinetic energy, involves an integral of the product of the ground state wave-function $\psi_o (x)$ and the second derivative of the ground state wave-function (all of which is multiplied by $-\hbar^2/(2m)$.
Carefully sketch the integrand as a function of x. Which regions of x are positive and which are negative? (This will be important.)
Wednesday, 2 pm: (i just added an extra-credit problem (10) which will be relevant to understanding molecules and crystals.)
Up to this point, we have focused a lot of our attention on wave-functions and degeneracy, and applied that to understanding the some of the periodic table and the geometry of bonding for a few elements (using the 1st-excited states of a -1/r potential).
At this point we can deepen our understanding of quantum physics by turning our attention to energy. Kinetic energy, particularly when associated with confinement, plays a huge role in the quantum world. The interplay and competition between kinetic and potential energy is very important to the phenomena of quantum physics. It can help us understand the size of quantum systems, including the hydrogen atom, the length of chemical bonds and why some materials are insulators instead of metals, as well as some other things. This assignment helps us begin that endeavor.
1. Referring to the enclosed (scanned) notes for clarification as needed,
a) graph exp[-rb/a] as a function of x along the x axis, where rb=sqrt[(x-b)^2+y^2+z^2]
b) do a contour plot to illustrate the nature of exp[-rb/a]
2.
a) graph exp[-r/a] + exp[-rb/a] as a function of x along the x axis.
b) do a contour plot to illustrate the nature of (exp[-r/a] + exp[-rb/a]).
3.
a) Calculate the expectation value of the kinetic energy (T) for the ground state of a 1D infinite square well.
b) Calculate the expectation value of the potential energy (U) for the ground state of a 1D infinite square well.
4. Note that one can calculate T without reference to any particular potential function. In the world of 1D quantum, consider an electron (of mass m) in a state in the form of a 1D normalized gaussian, i.e., $\psi (x) = (a \sqrt \pi)^{-1/2} e^{-x^2/2a^2}$:
a) calculate T (the expectation value of the kinetic energy) and,
b) graph the expectation value of T as a function of a.
5. On the other hand, potential energy (U) expectation values require both a potential, U(x) and a wave-function, $\psi(x)$.
a) Considering a as a parameter able to take on any positive, real value, calculate the expectation value of U for an electron in a state of the form $\psi (x) = (a \sqrt \pi)^{-1/2} e^{-x^2/2a^2}$, in a potential $U(x) = (1/2)kx^2$.
b) graph the expectation value of U as a function of a.
c) find the minimum of T + U (expectation values). At what value of a does that occur? What are the values of T and U at that minimum?
6. For a state that looks like the hydrogen atom electron ground state, but with a allowed to take any value (as in 4 and 5), one can show that T=$\hbar^2/(2ma^2)$ and that
U=$-e^2/a$ (see problem 8 for how one gets this). You can include a $1/(4 \pi \epsilon_o)$ if you prefer that unit system).
a) Show that $\hbar^2/(2ma^2)$ has units of energy,
b) Find the value of a that minimizes E=T + U and the value of T, U and E at that value of a.
c) Are E, T and U positive or negative? Why? (for each one)
7. Consider a 1D finite square well for which the potential is zero everywhere outside the well and -V inside the well. (V, the depth of our attractive well, is a positive number with units of energy.) Assume a width of L, and put the center of the well at x=0.
a) Assuming the ground state is of the form $A cos(kx)$ in the well (A and k undetermined) and $B e^{-\gamma (x-L/2)}$ outside the well, show that you can get a relation between k and $\gamma$ of the form -k*tan(kL/2) =$-\gamma$.
b) Additionally, gamma and k are related since $\hbar^2 k^2/2m = E + V$ and
$\hbar^2 \gamma^2 / (2m) = -E$ (where V is positive and E, the global separation parameter called the energy, is less than zero).
Write $\gamma$ as a function of V and k.
Why is E negative?
c) Anyway you can assume gamma is pretty much constant for small k (why?), and then graph the tan function and 1/k on the same graph to get the actual value of k for the ground state (graphically and approximately). Here is the question:
Is this value of k larger or smaller than the one you would get for an infinite square well of the same width?
d) and even more important: How do you explain that???
8. Extra credit. Calculate the expectation value of T for a hydrogen atom ground state wave function. (take 2 derivatives, integrate...). Do the same for U (i.e., integrate -1/r ...). (This is not actually that difficult as i thought at first since it is only radial derivatives and integrals, i think.)
9. Extra credit/Advanced problem. Consider an electron in a 1DHO in the mixed state sqrt(1/2)(Psi0(x,t) + Psi1(x,t)). Calculate and graph U and T (expectation values) as a function of t.
10. extra credit. For an electron in the ground state of a 1DHO, the calculation of T (the expectation value of the kinetic energy, involves an integral of the product of the ground state wave-function $\psi_o (x)$ and the second derivative of the ground state wave-function (all of which is multiplied by $-\hbar^2/(2m)$.
Carefully sketch the integrand as a function of x. Which regions of x are positive and which are negative? (This will be important.)
Friday, January 25, 2013
Homework 4 Discussion Problem.
In addition to the regular HW 4, you are invited to participate in the enclosed discussion problem related to creating sp4 bonding states. Please feel free also to bring up anything else related to sp3, sp4 and the geometry of molecular bonding in general.
How would you create sp4 states from the first excited states of hydrogen?
(Also, as an aside, I noticed that all the integrals of HW3 came down to doing one integral: the integral of x*Psi2r*Psi2x or, equivalently, the integral of y*Psi2r*Psi2y, each over all 3-D space.
In spherical co-ords one gets:
an integral of phi from 0 to 2pi, (which is pi),
an integral of theta from 0 to pi, (which is 4/3),
and an integral of [(r^5/2a) - r^4] exp(-r/a), which is 120a^6/(2a) - 24a^5 = 36a^5,
which is then divided by (8*pi*a^4) to get (48/8)a
= 6a.
Does that seem correct?)
How would you create sp4 states from the first excited states of hydrogen?
(Also, as an aside, I noticed that all the integrals of HW3 came down to doing one integral: the integral of x*Psi2r*Psi2x or, equivalently, the integral of y*Psi2r*Psi2y, each over all 3-D space.
In spherical co-ords one gets:
an integral of phi from 0 to 2pi, (which is pi),
an integral of theta from 0 to pi, (which is 4/3),
and an integral of [(r^5/2a) - r^4] exp(-r/a), which is 120a^6/(2a) - 24a^5 = 36a^5,
which is then divided by (8*pi*a^4) to get (48/8)a
= 6a.
Does that seem correct?)
Thursday, January 24, 2013
Jan 24 Class Notes -periodic table, sp2, bonding. (also integrating with wolfram alpha)
Here are some notes from these weeks classes. Please fell free to post any questions, comments, etc. here.
Here are some screen pics that illustrate how to integrate with Wolfram Alpha:
Here are some screen pics that illustrate how to integrate with Wolfram Alpha:
Outline
Here is a working outline for our class so you can have an idea what i am thinking about in terms of what we may be doing next (as well as what we have done and are focused on now). From time-to-time I can add discussion here regarding what you may wish to think about to prepare for our upcoming topics.
For example. I think the next topic coming up pretty soon is called energy and chemical bonding, but to study that one really needs to understand energy in quantum physics more generally. Just as in the physics 5 series, one can study energy by dividing it into two parts: kinetic and potential. These can abbreviate as K.E. and P.E., or just T and U. For example, what is the expectation value of the kinetic energy of an electron in the ground state of an infinite square well? How about its potential energy? Why does the ground state wave-function of a finite square well spill out beyond the edges of the well? What is the motivation for that? Closely related questions have to do with the size of the g.s. wave-fucntion for the harmonic oscillator or the hydrogen atom? Why are they not smaller?
Then we can consider how to construct molecular wave-functions (from atomic wave-functions) and what the benefit (in terms of energy) of that might be.
Your thoughts, comments and questions are welcome. (One thing to note is that we won't really use the time dependence until we get to the sections on quantum spectroscopy and lasers. For now, we are still focused on energy eigenstates (wave-functions), which are "stationary states".)
1D quantum theory:
-bound states of 1D systems
-time dependence and wave-like nature of 1D bound states
-time dependence of mixed states.
2D quantum theory:
-bound states of the 2DHO
-degeneracy
-time dependence of mixed states in 2D
3D quantum theory:
-bound states of the hydrogen atom (i.e., of an electron in a -1/r potential)
-degeneracy of the 1st excited states
-degeneracy, spin and the periodic table chemical
-bonding with the 1st excited states,
--sp2: Hexane, C2H4 sigma bonds (+ the pz orbital which can form pi bonds and delocalize)
--sp3: diamond and the structure of semiconductors (including Si, Ge, GaAs, GaAlP, GaN…
-H2O
- energy and chemical bonding (why H2 has a lower energy than H and H)
Quantum theory of semiconductors:
-back to 1D models
--2 square wells
--an infinite number of square wells
-electron states of spatially periodic systems
-Fermi statistics
Quantum spectroscopy:
-of a 1D sq well with N bound states
-stimulated absorption of a photon
-photoelectric effect spectroscopy (photoemission)
-spectroscopy of a hydrogen atom
--transitions between quantum states, selection rules
--fine structure (spin-orbit related splitting)
--atom in a magnetic or electric field (effect on degenerate states)
Lasers:
-Bose statistics
-stimulated emission of photons
-semiconductor lasers
Additional topics:
For example. I think the next topic coming up pretty soon is called energy and chemical bonding, but to study that one really needs to understand energy in quantum physics more generally. Just as in the physics 5 series, one can study energy by dividing it into two parts: kinetic and potential. These can abbreviate as K.E. and P.E., or just T and U. For example, what is the expectation value of the kinetic energy of an electron in the ground state of an infinite square well? How about its potential energy? Why does the ground state wave-function of a finite square well spill out beyond the edges of the well? What is the motivation for that? Closely related questions have to do with the size of the g.s. wave-fucntion for the harmonic oscillator or the hydrogen atom? Why are they not smaller?
Then we can consider how to construct molecular wave-functions (from atomic wave-functions) and what the benefit (in terms of energy) of that might be.
Your thoughts, comments and questions are welcome. (One thing to note is that we won't really use the time dependence until we get to the sections on quantum spectroscopy and lasers. For now, we are still focused on energy eigenstates (wave-functions), which are "stationary states".)
1D quantum theory:
-bound states of 1D systems
-time dependence and wave-like nature of 1D bound states
-time dependence of mixed states.
2D quantum theory:
-bound states of the 2DHO
-degeneracy
-time dependence of mixed states in 2D
3D quantum theory:
-bound states of the hydrogen atom (i.e., of an electron in a -1/r potential)
-degeneracy of the 1st excited states
-degeneracy, spin and the periodic table chemical
-bonding with the 1st excited states,
--sp2: Hexane, C2H4 sigma bonds (+ the pz orbital which can form pi bonds and delocalize)
--sp3: diamond and the structure of semiconductors (including Si, Ge, GaAs, GaAlP, GaN…
-H2O
- energy and chemical bonding (why H2 has a lower energy than H and H)
Quantum theory of semiconductors:
-back to 1D models
--2 square wells
--an infinite number of square wells
-electron states of spatially periodic systems
-Fermi statistics
Quantum spectroscopy:
-of a 1D sq well with N bound states
-stimulated absorption of a photon
-photoelectric effect spectroscopy (photoemission)
-spectroscopy of a hydrogen atom
--transitions between quantum states, selection rules
--fine structure (spin-orbit related splitting)
--atom in a magnetic or electric field (effect on degenerate states)
Lasers:
-Bose statistics
-stimulated emission of photons
-semiconductor lasers
Additional topics:
1D quantum resummary.
I made this video after a student let me know that they were feeling pretty lost and confused. It summarizes just what you need to know now in order to be able to make sense of what we are doing in class (with the 1st excited states of the -1/r potential in 3D). It focuses on making "off-center states" through combinations of states, which is what we are working on currently with the H-atom 1st excited states, and is very important to understanding quantum physics and chemistry. Please feel free to post any questions here.
Saturday, January 19, 2013
Homework 3: sp2 bonding from 1st excited states.
(due Friday Jan 25 by 3 PM )
1. Graph the (spatial) wave-functions Psi1r and Psi2r as a function of r. (Note that r cannot be negative.) Where is "a" in your graph?
2. Graph Psi1r and Psi2r as a function of x along the line y=z=0 (i.e., the x axis). Indicate where "a" is in your graph.
3. Graph Psi2x as a function of x along the line y=z=0 (i.e., the x axis). Why is it pointless to graph Psi2x along the y or z axis?
4. Illustrate the nature of Psi2x using either a polar plot or contour plot of the x-y plane.
(This is an important problem!)
5. Calculate the expectation value of x for:
a) an electron in the state Psi2r,
b) an electron in the state Psi2x,
c) an electron in the state (sqrt(1/3)*Psi2r + sqrt(2/3)*Psi2x)
6. a) Calculate the expectation values of x and y, respectively, (2 different calculations) for an electron in the state (sqrt(1/3)*Psi2r - sqrt(1/6)*Psi2x+ sqrt(1/2)*Psi2y).
**Please note that there was a critical typo in this problem. See discussion below to get an idea where the error was. (This error propagated into 8 and 10.)
7. For which of the states in problems 5 and 6 would the expectation values (of x or y) be time dependent? Are you sure? Explain.
8. Calculate the expectation value of y for an electron in the state (sqrt(1/3)*Psi2r + sqrt(2/3)*Psi2x) and then, on a graph where the axes are the x-y plane indicate, as a dot:
i) the location of the (x,y) expectation values for that state (sqrt(1/3)*Psi2r + sqrt(2/3)*Psi2x),
ii) the location of the (x,y) expectation values for the state (sqrt(1/3)*Psi2r - sqrt(1/6)*Psi2x+ sqrt(1/2)*Psi2y).
(This is a fairly important problem to do carefully and understand.)
9. never mind.
10. Advanced. Are the states:
(sqrt(1/3)*Psi2r + sqrt(2/3)*Psi2x) and
(sqrt(1/3)*Psi2r - sqrt(1/6)*Psi2x+ sqrt(1/2)*Psi2y)
orthogonal (in the sense of the inner product we discussed involving integrals over 3D space)? (For that determination you may assume that Psi2r, Psi2x and Psi2y are mutually orthogonal.)
11. Can you find another one or two states that have an energy E2 (1st excited states) and that are orthogonal to the 2 states in problem 10 (and to each other)?
12. Optional graph, thought and discussion problem. Please post any thoughts, questions or results for this problem here:
Suppose you do not like to do grungy calculations and integrals, but you want to get an idea of whether the expectation value of x is positive, negative or zero for the state sqrt(1/2)[Psi2r+Psi2x]. Can you perhaps graph that along just the x-axis (where y and z are zero)? (Why is that a pretty easy graph?) Can you then guess as to whether the expectation value of x is positive, negative or zero from looking at that graph?
Solutions follow:
1. Graph the (spatial) wave-functions Psi1r and Psi2r as a function of r. (Note that r cannot be negative.) Where is "a" in your graph?
2. Graph Psi1r and Psi2r as a function of x along the line y=z=0 (i.e., the x axis). Indicate where "a" is in your graph.
3. Graph Psi2x as a function of x along the line y=z=0 (i.e., the x axis). Why is it pointless to graph Psi2x along the y or z axis?
4. Illustrate the nature of Psi2x using either a polar plot or contour plot of the x-y plane.
(This is an important problem!)
5. Calculate the expectation value of x for:
a) an electron in the state Psi2r,
b) an electron in the state Psi2x,
c) an electron in the state (sqrt(1/3)*Psi2r + sqrt(2/3)*Psi2x)
6. a) Calculate the expectation values of x and y, respectively, (2 different calculations) for an electron in the state (sqrt(1/3)*Psi2r - sqrt(1/6)*Psi2x+ sqrt(1/2)*Psi2y).
**Please note that there was a critical typo in this problem. See discussion below to get an idea where the error was. (This error propagated into 8 and 10.)
7. For which of the states in problems 5 and 6 would the expectation values (of x or y) be time dependent? Are you sure? Explain.
8. Calculate the expectation value of y for an electron in the state (sqrt(1/3)*Psi2r + sqrt(2/3)*Psi2x) and then, on a graph where the axes are the x-y plane indicate, as a dot:
i) the location of the (x,y) expectation values for that state (sqrt(1/3)*Psi2r + sqrt(2/3)*Psi2x),
ii) the location of the (x,y) expectation values for the state (sqrt(1/3)*Psi2r - sqrt(1/6)*Psi2x+ sqrt(1/2)*Psi2y).
(This is a fairly important problem to do carefully and understand.)
9. never mind.
10. Advanced. Are the states:
(sqrt(1/3)*Psi2r + sqrt(2/3)*Psi2x) and
(sqrt(1/3)*Psi2r - sqrt(1/6)*Psi2x+ sqrt(1/2)*Psi2y)
orthogonal (in the sense of the inner product we discussed involving integrals over 3D space)? (For that determination you may assume that Psi2r, Psi2x and Psi2y are mutually orthogonal.)
11. Can you find another one or two states that have an energy E2 (1st excited states) and that are orthogonal to the 2 states in problem 10 (and to each other)?
12. Optional graph, thought and discussion problem. Please post any thoughts, questions or results for this problem here:
Suppose you do not like to do grungy calculations and integrals, but you want to get an idea of whether the expectation value of x is positive, negative or zero for the state sqrt(1/2)[Psi2r+Psi2x]. Can you perhaps graph that along just the x-axis (where y and z are zero)? (Why is that a pretty easy graph?) Can you then guess as to whether the expectation value of x is positive, negative or zero from looking at that graph?
Solutions follow:
Friday, January 18, 2013
Jan 17 Class Notes.
These notes summarize some of what we covered this week, Jan 15 and 17, especially the ways of summarizing the 1st excited states (of the H-atom potential) that we explored on the 17th. Please let me know of you would be interested in a video discussing anything about these states.
Perhaps it might seem like we went to a lot of trouble and effort to delve into these states (the first excited states) in a lot of confusing detail. After all, isn't this just one of many such degeneracy manifolds? How important could it really be? Well, I think it is extremely important. Understanding these 4 degenerate states (in their different manifestations) really well is the key to understanding the most important aspects of the periodic table, as well as the structures of molecules such as H2O, CH4, C6H6, etc., not to mention semiconductors. Within these states lies the key to understanding some of the most important things in our world.
Perhaps it might seem like we went to a lot of trouble and effort to delve into these states (the first excited states) in a lot of confusing detail. After all, isn't this just one of many such degeneracy manifolds? How important could it really be? Well, I think it is extremely important. Understanding these 4 degenerate states (in their different manifestations) really well is the key to understanding the most important aspects of the periodic table, as well as the structures of molecules such as H2O, CH4, C6H6, etc., not to mention semiconductors. Within these states lies the key to understanding some of the most important things in our world.
Thursday, January 17, 2013
LSS Tutoring Available.
Here is a note I got from Eric Reichwein regarding availability of tutoring for this class at no cost.
The website to sign up for tutoring is http://www2.ucsc.edu/lss/
There are some times that I posted for possible sessions, but please let the students know that I can schedule more if they can't make any of the times I posted already. And most importantly that its a free resource for them. Thanks,
Eric Reichwein
Tuesday, January 15, 2013
Discussion Section and Office Hours.
There will be a Discussion Section led by your TA, TJ Torres, who is a very advanced graduate student, on:
Wednesday, 6-7 PM, ISB 231.
Also, I will have an office hour tomorrow (Weds) at noon (12-1 PM) in ISB 243, and then another one on Friday from 2-3 PM (also in ISB 243). With regard to my office hours, I would like to ask a special consideration: because my health and immune system is somewhat compromised, please consider that and we should avoid proximity and contact if you might be sick or feel like you may be coming down with something. Thanks very much. Your consideration with this is really appreciated!
Wednesday, 6-7 PM, ISB 231.
Also, I will have an office hour tomorrow (Weds) at noon (12-1 PM) in ISB 243, and then another one on Friday from 2-3 PM (also in ISB 243). With regard to my office hours, I would like to ask a special consideration: because my health and immune system is somewhat compromised, please consider that and we should avoid proximity and contact if you might be sick or feel like you may be coming down with something. Thanks very much. Your consideration with this is really appreciated!
Saturday, January 12, 2013
Homework 2: Due Friday, Jan 18, by 3 PM.
Before you tackle this homework, it may be helpful for you to review and understand the video Review 1D QM: part 2 (in the 1st post on this blog), if you have not already done so. 2DHO states can be built from products of the 1DHO states which are presented and discussed in that video; (the Jan 10 class summary is also relevant).
One of the the key goals of this homework assignment is to learn about quantum degeneracy, that is, the occurrence of orthogonal states (wave-functions) which have the same energy (and hence the same time dependence).
1.
a) Write the (normalized wave-function of an electron in the) ground state of the 2-dimensional harmonic oscillator.
b) What is its energy?
2.
a) Write the 1st excited states of the 2-dimensional harmonic oscillator.
b) What is their energy?
c) How many are there?
3.
a) Write the 2nd excited states of the 2-dimensional harmonic oscillator.
b) What is their energy?
c) How many are there?
4 & 5 have been deleted because of concern that that might take be an unnecessary distraction that would take time away from more important problems.
Bonus Problem: Come up with a (simple) way to illustrate the nature of some or all of these states; something that illustrates where the wave-function (at t=0) tends to be large, and where it is not. Perhaps think about including some way to distinguish where the wave function is positive and where it is negative (phase). You can use sketches, color, surfaces of constant amplitude, polar plots, 2-dimensional contour plots or whatever you come up with.
6.
a) What is the normalized wave-function of an electron in the ground state of a e^2/r potential in 3 dimensions (i.e., a hydrogen atom). (You can include the 1/(4*pi*epsilon0 factor as you like.)
b) What is its energy?
7.
a) What are some normalized wave-function of an electron in the 1st excited states of a e^2/r potential in 3 dimensions (i.e., a hydrogen atom). (You can include the 1/(4*pi*epsilon0 factor as you like.)
b) What is the energy of those states?
c) How many are there?
8. extra credit. advanced.
For an electron in a 2DHO potential in the state which is an equal mix (normalized) of the ground state, Psi00, and the first excited state Psi10, calculate the expectation values of x, and y, respectively, as a function of time.
9. extra credit. very advanced.
For an electron in a 2DHO potential in the state which is an equal mix (normalized) of the ground state, Psi00, and the first excited state (Psi10 + i Psi01)/sqrt(2), calculate the expectation values of x, and y, respectively, as a function of time. What do you observe? What is this calculation trying to tell you? (This normalized mixed state is [Psi00 + (Psi10 + i*Psi01)/sqrt(2)]/sqrt(2).)
10. extra credit. Very, very advanced.
For an electron in the 1st excited state (Psi10 + i*Psi01)/sqrt(2), calculate the (z component of the) angular momentum using Lz = X Py - Y Px. (see 1st comment below)
10-background. an optional extra problem. Because of an interest expressed in momentum expectation values, here is something you can do for fun that may provide a good warm-up problem for 10.
-Calculate the expectation values of p and of p^2 for the ground state of the infinite square well.
(aside: what is p? How do you calculate its expectation value?)
-If you are feeling ambitious and you like derivatives, do the same for the ground state of the harmonic oscillator.
Any suggestions for problems are most welcome and can be posted here. I mean that! (and though I might be surprised, it would be a very pleasant surprise).
Please post your questions here. The only bad questions are the ones that go unasked :( . I am sure if you have a question, a lot of other people are wondering the same thing. Also, you can become a follower of this site. Some people use made up whimsical profiles, some use their real name. It is entirely up to you. This is your education. I encourage you to make the most of it.
One of the the key goals of this homework assignment is to learn about quantum degeneracy, that is, the occurrence of orthogonal states (wave-functions) which have the same energy (and hence the same time dependence).
1.
a) Write the (normalized wave-function of an electron in the) ground state of the 2-dimensional harmonic oscillator.
b) What is its energy?
2.
a) Write the 1st excited states of the 2-dimensional harmonic oscillator.
b) What is their energy?
c) How many are there?
3.
a) Write the 2nd excited states of the 2-dimensional harmonic oscillator.
b) What is their energy?
c) How many are there?
4 & 5 have been deleted because of concern that that might take be an unnecessary distraction that would take time away from more important problems.
Bonus Problem: Come up with a (simple) way to illustrate the nature of some or all of these states; something that illustrates where the wave-function (at t=0) tends to be large, and where it is not. Perhaps think about including some way to distinguish where the wave function is positive and where it is negative (phase). You can use sketches, color, surfaces of constant amplitude, polar plots, 2-dimensional contour plots or whatever you come up with.
6.
a) What is the normalized wave-function of an electron in the ground state of a e^2/r potential in 3 dimensions (i.e., a hydrogen atom). (You can include the 1/(4*pi*epsilon0 factor as you like.)
b) What is its energy?
7.
a) What are some normalized wave-function of an electron in the 1st excited states of a e^2/r potential in 3 dimensions (i.e., a hydrogen atom). (You can include the 1/(4*pi*epsilon0 factor as you like.)
b) What is the energy of those states?
c) How many are there?
8. extra credit. advanced.
For an electron in a 2DHO potential in the state which is an equal mix (normalized) of the ground state, Psi00, and the first excited state Psi10, calculate the expectation values of x, and y, respectively, as a function of time.
9. extra credit. very advanced.
For an electron in a 2DHO potential in the state which is an equal mix (normalized) of the ground state, Psi00, and the first excited state (Psi10 + i Psi01)/sqrt(2), calculate the expectation values of x, and y, respectively, as a function of time. What do you observe? What is this calculation trying to tell you? (This normalized mixed state is [Psi00 + (Psi10 + i*Psi01)/sqrt(2)]/sqrt(2).)
10. extra credit. Very, very advanced.
For an electron in the 1st excited state (Psi10 + i*Psi01)/sqrt(2), calculate the (z component of the) angular momentum using Lz = X Py - Y Px. (see 1st comment below)
10-background. an optional extra problem. Because of an interest expressed in momentum expectation values, here is something you can do for fun that may provide a good warm-up problem for 10.
-Calculate the expectation values of p and of p^2 for the ground state of the infinite square well.
(aside: what is p? How do you calculate its expectation value?)
-If you are feeling ambitious and you like derivatives, do the same for the ground state of the harmonic oscillator.
Any suggestions for problems are most welcome and can be posted here. I mean that! (and though I might be surprised, it would be a very pleasant surprise).
Please post your questions here. The only bad questions are the ones that go unasked :( . I am sure if you have a question, a lot of other people are wondering the same thing. Also, you can become a follower of this site. Some people use made up whimsical profiles, some use their real name. It is entirely up to you. This is your education. I encourage you to make the most of it.
Friday, January 11, 2013
January 10 class notes: our first degeneracy manifold.
Here is a summary of our Thursday, Jan 10 class. The key thing about this class is not so much that we looked at a few states associated with the 2DHO, but rather that we encountered and began to explore our first degeneracy manifold.
One can easily miss the forest while focusing on the trees, so let me try to summarize the essence of what we have done so far this quarter:
1) Examined the nature of a few low-energy quantum bound states (for an electron in a HO or an inf. sq. well potential),
2) Looked at quantum time dependence (in the context of a mixed state),
3) Encountered a degeneracy manifold (in the context of a 2DHO).
Everything we are doing now is part of a foundation for what we will learn and explore later in the quarter.
One can easily miss the forest while focusing on the trees, so let me try to summarize the essence of what we have done so far this quarter:
1) Examined the nature of a few low-energy quantum bound states (for an electron in a HO or an inf. sq. well potential),
2) Looked at quantum time dependence (in the context of a mixed state),
3) Encountered a degeneracy manifold (in the context of a 2DHO).
Everything we are doing now is part of a foundation for what we will learn and explore later in the quarter.
Thursday, January 10, 2013
HW 1 & HW 1 Solutions.
Above please find still images of HW1 (from the HW 1 post videos).
Additionally, the following are some solution notes related to HW 1. There is some randomness to the page order that i can't control, but you can infer the order from the problem numbers. Please feel free to question or discuss the solutions here.
Tuesday, January 8, 2013
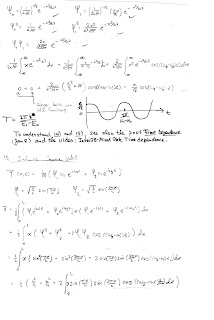
Time Dependence
These videos are intended to enhance your understanding of time dependence in quantum mechanics. They may help you with problems 14-16 on the homework. The 1st video looks at the fundamental nature of the quantum wave that emerges from the Schroedinger Wave Equation. The 2nd and 3rd videos examines the time dependence of a "mixed" (non-stationary) state in which the wave moves from side to side. The 2nd video provides a start to calculating the expectation value of x; the 3rd video contains a graphic portrayal of the nature of the mixed state. (The problem with the 3rd video has been fixed. You can see the entire graph now.) Comments, questions and discussion posted here are most welcome.
The nature of the quantum wave:
Calculating x:
Time dependence of a mixed-state wave function:
The nature of the quantum wave:
Calculating x:
Time dependence of a mixed-state wave function:
Subscribe to:
Comments (Atom)